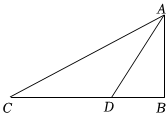
 在學習直角三角形的過程中,小明遇到了一個問題:在直角三角形ABC中,∠B=90°,AD平分∠CAB,探究AC,AB,CD,DB是否成比例線段,小明的思路是:首先過點D作AC的垂線,從而構造與△ADB全等的三角形,再通過三角形面積建立等量關系,使問題得到解決.請根據小明的思路完成下面的作圖與填空:
在學習直角三角形的過程中,小明遇到了一個問題:在直角三角形ABC中,∠B=90°,AD平分∠CAB,探究AC,AB,CD,DB是否成比例線段,小明的思路是:首先過點D作AC的垂線,從而構造與△ADB全等的三角形,再通過三角形面積建立等量關系,使問題得到解決.請根據小明的思路完成下面的作圖與填空:
尺規作圖:過點D作DE⊥AC于點E(用基本作圖,保留作圖痕跡,不寫作法、結論).
證明:∵AD平分∠CAB,
∴①∠EAD=∠BAD①∠EAD=∠BAD,
∵DE⊥AC,
∴②∠DEA=90°②∠DEA=90°,
∴∠DEA=∠B,
在△ADE和△ADB中,
∠DEA=∠B ∠EAD=∠BAD ③
,
∴△ADE≌△ADB(AAS),
∴④DE=DB④DE=DB,
又∵∠DEA=∠B=90°,
∴S△ADC=12CD?AB=12AC?DE,
∴CD?AB=AC?DE=⑤2S△ADC⑤2S△ADC,
即ACAB=CDDB,
∴AC,AB,CD,DB為成比例線段.
∠ DEA =∠ B |
∠ EAD =∠ BAD |
③ |
S
△
ADC
=
1
2
CD
1
2
AC
?
DE
AC
AB
=
CD
DB
【答案】①∠EAD=∠BAD;②∠DEA=90°;④DE=DB;⑤2S△ADC
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/22 8:30:1組卷:55引用:1難度:0.6
相似題
-
 1.如圖,在△ABC中,點D、E、F分別在邊AB、AC、BC上,DE∥BC,EF∥AB.如果DE:BC=2:5,那么EF:AB的值是 .發布:2025/5/24 12:0:1組卷:207引用:2難度:0.5
1.如圖,在△ABC中,點D、E、F分別在邊AB、AC、BC上,DE∥BC,EF∥AB.如果DE:BC=2:5,那么EF:AB的值是 .發布:2025/5/24 12:0:1組卷:207引用:2難度:0.5 -
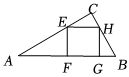 2.如圖,在△ABC中,∠C=90°,正方形EFGH的邊FG在△ABC的邊AB上,頂點E、H分別在邊AC、BC上,如果其面積為24,那么AF?BG的值為 .發布:2025/5/24 12:30:1組卷:237引用:3難度:0.6
2.如圖,在△ABC中,∠C=90°,正方形EFGH的邊FG在△ABC的邊AB上,頂點E、H分別在邊AC、BC上,如果其面積為24,那么AF?BG的值為 .發布:2025/5/24 12:30:1組卷:237引用:3難度:0.6 -
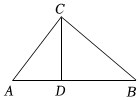 3.如圖,在△ABC中,CD⊥AB,垂足為點D,以下條件中不能推出△ABC為直角三角形的是( )
3.如圖,在△ABC中,CD⊥AB,垂足為點D,以下條件中不能推出△ABC為直角三角形的是( )A.∠A=∠BCD B. =CDADBDCDC. =ACBCCDBDD. =ACBCADBD發布:2025/5/24 12:30:1組卷:185引用:4難度:0.5
相關試卷


