綜合與實踐
問題情境：已知正方形ABCD邊長為1，G是AB邊的中點，E是射線DC上的一個動點．
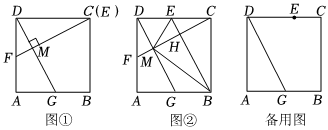
解決問題：（1）如圖①，若點E與點C重合，過點E作EF⊥DG于點M，交AD邊于點F，判斷線段EF與DG的數量關系，并說明理由；
初步探究：（2）如圖②，若點E在線段DC上且點E與點C不重合，連接BE，將△BCE沿著BE翻折，使點C落在DG上的點M處，連接CM并延長交AD邊于點F且CF⊥DG，求EH?CF的值；
深入探究：（3）若點E與點C不重合，以點C為圓心，線段GE的長為半徑作⊙C，請探究點E運動到什么位置時，⊙C與線段DG只有一個公共點．
【考點】圓的綜合題．
【答案】（1）EF=DG，理由見解答；
（2）EH?CF=；
（3）當點E運動到DC中點的右側時，⊙C與線段DG只有一個公共點．
（2）EH?CF=
1
4
（3）當點E運動到DC中點的右側時，⊙C與線段DG只有一個公共點．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：88引用：1難度：0.4
相似題
-
1．在半徑為5的圓中，弦AB=8，點C是劣弧AB上的動點（可與A、B重合），連接OC交AB于點P．
（1）如圖1，當OC⊥AB時，求OP的長度；
（2）如圖2，過C點作CM⊥AB，垂足為點M，設CM=m,求OP的長度（用含m的式子表示），并指出m的取值范圍；
（3）如圖3，設CM=m,連接OM．求OM2+8CM的取值范圍．
發布：2025/5/26 7:30:2組卷：379引用：1難度：0.3 -
2．如圖，△ABC內接于圓O，高AD、CE相交于點H，延長AH交圓O于點G．
（1）如圖1，求證：DG=DH；
（2）如圖2，連接CO，求證：∠BCO=∠HCA；
（3）如圖3，在（2）的條件下，延長CO交圓O于點N，連接GN、DE，若，CD=1，求DH的長．NG=2DE=210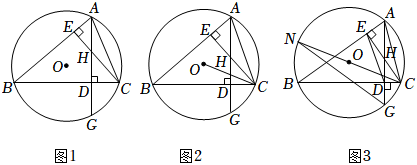
發布：2025/5/26 7:30:2組卷：69引用：1難度：0.2 -
3．已知四邊形ABCD為⊙O內接四邊形，對角線AC、BD相交于點E，AD=ED．
（1）如圖1，求證：BC=EC；
（2）如圖2，弦BD過圓心，過點A作AF⊥BD于H，求證：∠BDC=∠CAF；
（3）如圖3，在（2）的條件下，連接BF，交弦CD于點M，連接MO，若∠ACD+2∠BOM=180°，DH=，求線段OM的長．655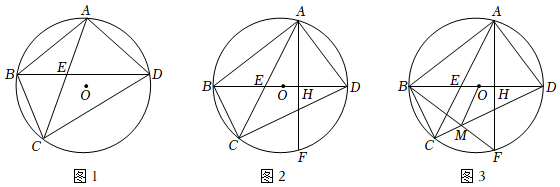
發布：2025/5/26 7:30:2組卷：101引用：1難度：0.2