在△ABC中，AB=BC=2，∠ABC=120°，將△ABC繞點B順時針旋轉角α（0°＜α＜90°）得△A1BC1，A1B交AC于點E，A1C1分別交AC、BC于D、F兩點．
（1）如圖1，觀察并猜想，在旋轉過程中，線段BE與BF有怎樣的數量關系？并證明你的結論；
（2）如圖2，當α=30°時，試判斷四邊形BC1DA的形狀，并說明理由．
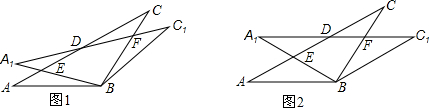
【考點】旋轉的性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/27 2:0:8組卷：1608引用：17難度：0.3
相似題
-
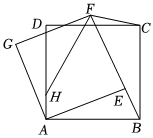1．如圖，在正方形ABCD中，AB=8，點H在AD上，且AH=2，點E繞著點B旋轉，且BE=3，在AE的上方作正方形AEFG，則線段FH的最小值是 ．發布：2025/5/25 10:0:1組卷：470引用：1難度：0.3 -
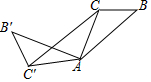2．如圖，在△ABC中，∠CAB=30°，將△ABC在平面內繞點A逆時針旋轉到△AB'C'的位置，且CC'∥AB，則旋轉角的度數為（ ）發布：2025/5/25 8:30:2組卷：1249引用：13難度：0.8 -
3．如圖，將△ABC繞點C順時針旋轉得到△EDC，若點A恰好在ED的延長線上，∠BAC=40°，則∠BAE的度數為（ ）發布：2025/5/25 9:0:1組卷：723引用：12難度：0.7