四邊形ABCD中，AB=BC=CD=AD，∠DAB=60°，點E是AD邊的中點，點M是AB邊上的一個動點（不與點A重合），連接ME并延長交CD的延長線于點N，連接MD，AN．
（1）求證：四邊形AMDN是平行四邊形；
（2）當AM=12AB時，四邊形AMDN是什么特殊四邊形？請說明理由．
AM
=
1
2
AB
【考點】菱形的性質；平行四邊形的判定與性質．
【答案】（1）證明過程見解答；
（2）平行四邊形AMDN是矩形，理由見解答．
（2）平行四邊形AMDN是矩形，理由見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/11 8:0:9組卷：79引用：1難度：0.5
相似題
-
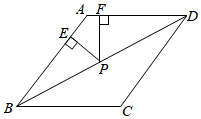1．如圖，菱形ABCD的周長為40，面積為80，P是對角線BD上一點，分別作P點到直線AB、AD的垂線段PE、PF，則PE+PF等于 ．發布：2025/5/25 5:30:2組卷：750引用：4難度：0.5 -
2．如圖，在菱形ABCD中，∠D=60°，E是AD上一點，M、N分別是CE、AE的中點，且MN=2，求菱形ABCD的周長．發布：2025/5/25 2:0:6組卷：74引用：1難度：0.5 -
3．如圖，在菱形ABCD中，對角線AC，BD相交于點O，AC=8，BD=6，點E，F分別為AO，DO的中點，則線段EF的長為 ．發布：2025/5/25 4:0:1組卷：88引用：2難度：0.5