下列命題：如圖，正方形ABCD中，E、F分別為AB、AD上的點(diǎn)，AF=BE，CE、BF交于H，BF交AC于M，O為AC的中點(diǎn)，OB交CE于N，連OH．下列結(jié)論中：①BF⊥CE；②OM=ON；③OH=12CN；④2OH+BH=CH．其中正確的命題有（ ）
OH
=
1
2
CN
2
OH
+
BH
=
CH
【答案】B
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/29 8:0:9組卷：1193引用：12難度：0.9
相似題
-
1．如圖，正方形ABCD及正方形AEFG，連接BE、CF、DG．則BE：CF：DG等于（ ）發(fā)布：2025/5/28 0:30:1組卷：653引用：6難度：0.7 -
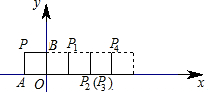
2．如圖，將邊長(zhǎng)為1的正方形OAPB沿x軸正方向連續(xù)翻轉(zhuǎn)2012次，點(diǎn)P依次落在點(diǎn)P1，P2，P3，P4，…，P2012的位置，則P2012的橫坐標(biāo)x2012=（ ）
發(fā)布：2025/5/28 0:30:1組卷：202引用：2難度：0.9 -
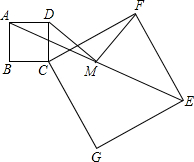3．如圖，正方形ABCD和正方形CGEF（CG＞BC），連接AE，取線段AE的中點(diǎn)M．
證明：FM⊥MD，且FM=MD．發(fā)布：2025/5/28 1:30:2組卷：1262引用：2難度：0.1