勾股定理是人類早期發現并證明的重要數學定理之一，是用代數思想解決幾何問題的最重要的工具之一，也是數形結合的紐帶之一，它不但因證明方法層出不窮吸引著人們，更因為應用廣泛而使人入迷．
（1）證明勾股定理
據傳當年畢達哥拉斯借助如圖3所示的兩個圖驗證了勾股定理，請你說說其中的道理．
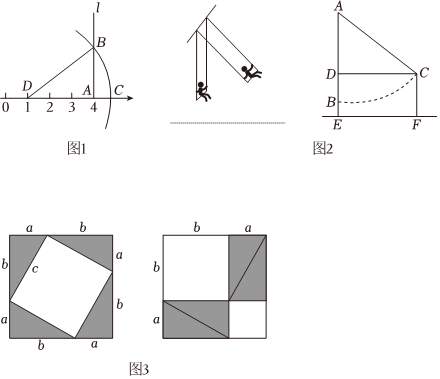
（2）應用勾股定理
①應用場景1——在數軸上畫出表示無理數的點．
如圖1，在數軸上找出表示4的點A，過點A作直線l垂直于DA，在l上取點B，使AB=2，以點D為圓心，DB為半徑作弧，則弧與數軸的交點C表示的數是 13+113+1．
②應用場景2——解決實際問題．
如圖2，鄭州某公園有一秋千，秋千靜止時，踏板離地的垂直高度BE=0.5m,將它往前推2m至C處時，水平距離CD=2m,踏板離地的垂直高度CF=1.5m,它的繩索始終拉直，求繩索AC的長．
13
13
【答案】+1
13
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/3 8:0:9組卷：350引用：5難度：0.5
相似題
-
1．公元三世紀，我國漢代數學家趙爽在注解《周髀算經》時給出的“趙爽弦圖”如圖所示，它是由四個全等的直角三角形與中間的小正方形拼成的一個大正方形．如果大正方形的面積是125，小正方形面積是25，則tanθ的值為（ ）發布：2025/5/23 22:0:2組卷：95引用：2難度：0.6 -
2．?我國古代數學家趙爽巧妙地用“弦圖”證明了勾股定理，標志著中國古代的數學成就．如圖，若弦圖中四個全等的直角三角形的兩條直角邊長分別為3和4，則中間小正方形的對角線長為 ．發布：2025/5/23 3:30:1組卷：151引用：1難度：0.8 -
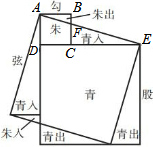3．魏晉時期，偉大數學家劉徽利用如圖通過“以盈補虛，出入相補”的方法，即“勾自乘為朱方，股自乘為青方，令出入相補，各從其類”證明了勾股定理，若圖中BF=2，CF=4，則AE的長為．發布：2025/5/23 19:0:2組卷：801引用：5難度：0.5