閱讀下面材料，完成（1），（2）兩題
數(shù)學(xué)課上，老師出示了這樣一道題：如圖1，在△ABC中，AB=AC，∠BAC=120°，點(diǎn)D為AB上一點(diǎn)，且滿足BD=AD，E為CD上一點(diǎn)，∠AEC=60°，延長(zhǎng)AE交BC于F，求AEEF的值．同學(xué)們經(jīng)過(guò)思考后，交流了自己的想法：
小明：“通過(guò)觀察和度量，發(fā)現(xiàn)∠BAF與∠ACD相等．”
小偉：“通過(guò)構(gòu)造全等三角形，經(jīng)過(guò)進(jìn)一步推理，就可以求出AEEF的值．”
…
老師：“把原題條件中的‘BD=AD′，改為‘BD=kAD′其他條件不變（如圖2），也可以求出AEEF的值．”
（1）在圖1中，①求證：∠BAF=∠ACD；②求出AEEF的值；
（2）如圖2，若BD=kAD，直接寫出AEEF的值（用含k的代數(shù)式表示）．
AE
EF
AE
EF
AE
EF
AE
EF
AE
EF
【考點(diǎn)】相似形綜合題．
【答案】（1）①證明見(jiàn)解析；②；
（2）．
4
3
（2）
k
+
3
k
2
+
2
k
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：205引用：1難度：0.1
相似題
-
1．平行四邊形ABCD中，點(diǎn)C關(guān)于AD的對(duì)稱點(diǎn)為E，連接DE，BE，BE交AD于點(diǎn)F．
（1）如圖1，若∠ADC=90°，試說(shuō)明點(diǎn)F為BE的中點(diǎn)；
（2）如圖2，若∠ABC=α（0°＜α＜90°）．
①試判斷點(diǎn)F是否為BE的中點(diǎn)？并說(shuō)明理由；
②若∠ABC=45°，延長(zhǎng)BA，DE交于點(diǎn)H，求的值．DFBH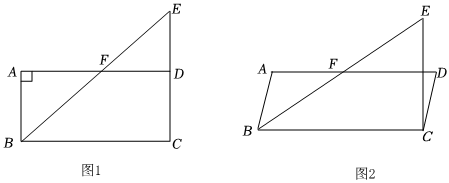
發(fā)布：2025/6/5 19:30:2組卷：241引用：4難度：0.1 -
2．已知△ABC為等腰直角三角形，∠BAC=90°，AC=AB=1，點(diǎn)D為線段BC的中點(diǎn)，∠BCA的外角∠BCH的平分線與∠DAC的平分線交于點(diǎn)E，與AD的延長(zhǎng)線交于點(diǎn)F，連接BE．
（1）如圖1，求∠AEB的度數(shù)；
（2）如圖2，將線段CF繞點(diǎn)F逆時(shí)針旋轉(zhuǎn)至90°點(diǎn)G，連接BG，求的值；BGAC
（3）如圖3，點(diǎn)G關(guān)于線段CF的對(duì)稱點(diǎn)為點(diǎn)M，點(diǎn)P在直線AB上運(yùn)動(dòng)，請(qǐng)直接寫出PM+2PC的最小值．發(fā)布：2025/6/5 21:0:1組卷：137引用：2難度：0.6 -
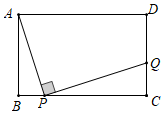3．如圖，在矩形ABCD中，點(diǎn)P是BC邊上任意一點(diǎn)（點(diǎn)P不與B、C重合），連接AP，作PQ⊥AP，交CD于點(diǎn)Q，若AB=3，BC=4．
（1）試證明：△ABP∽△PCQ；
（2）當(dāng)BP為多少時(shí)，CQ最長(zhǎng)，最長(zhǎng)是多少？
（3）試探究，是否存在一點(diǎn)P，使△APQ是等腰直角三角形？發(fā)布：2025/6/6 4:0:1組卷：209引用：4難度：0.2