如圖（1），大正方形的面積可以表示為（a+b）2，同時大正方形的面積也可以表示成兩個小正方形面積與兩個長方形的面積之和，即a2+2ab+b2．同一圖形（大正方形）的面積，用兩種不同的方法求得的結果應該相等，從而驗證了完全平方公式：
（a+b）2=a2+2ab+b2．
把這種“同一圖形的面積，用兩種不同的方法求出的結果相等，從而構建等式，根據等式解決相關問題”的方法稱為“面積法”．
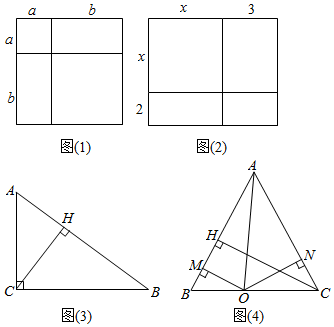
（1）用上述“面積法”，通過如圖（2）中圖形的面積關系，直接寫出一個多項式進行因式分解的等式：x2+5x+6=（x+3）（x+2）x2+5x+6=（x+3）（x+2）．
（2）如圖（3），Rt△ABC中，∠C=90°，CA=3，CB=4，CH是斜邊AB邊上的高．用上述“面積法”求CH的長；
（3）如圖（4），等腰△ABC中，AB=AC，點O為底邊BC上任意一點，OM⊥AB，ON⊥AC，CH⊥AB，垂足分別為點M，N，H，連接AO，用上述“面積法”求證：OM+ON=CH．
【考點】三角形綜合題．
【答案】x2+5x+6=（x+3）（x+2）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：685引用：5難度：0.5
相似題
-
1．性質探究
如圖（1），在等腰三角形ABC中，∠ACB=120°，則底邊AB與腰AC的長度之比為．
理解運用
（1）若頂角為120°的等腰三角形的周長為4+2，則它的面積為；3
（2）如圖（2），在四邊形EFGH中，EF=EG=EH，在邊FG，GH上分別取中點M，N，連接MN．若∠FGH=120°，EF=20，求線段MN的長．
類比拓展
頂角為2α的等腰三角形的底邊與一腰的長度之比為．（用含α的式子表示）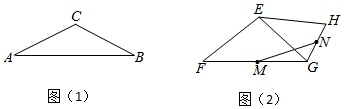
發布：2025/5/24 21:30:1組卷：815引用：4難度：0.2 -
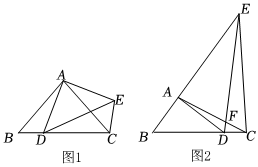2．如圖，Rt△ABC與Rt△ADE的直角頂點重合于點A，點D在BC邊上（不與B，C重合）．
（1）如圖1，當∠ABC=∠ADE=45°時，請直接寫出線段BD，CE之間的數量關系．
（2）如圖2，當∠ABC=∠ADE=60°時，設AC與DE交于點F．①求證EC=BD．②若BD=3，DC=1，試分別探求tan∠FDC和3的值．FDFC發布：2025/5/24 21:30:1組卷：21引用：1難度：0.2 -
3．問題情景：已知在△ABC中，AB=AC，∠BAC=α，過點A作AD⊥BC于點D，點P為直線BC上一點（不與點B、C重合），過點P作PM⊥AB于點M，PN⊥AC于點N．
（1）觀察猜想
如圖1，若α=60°，P在線段BC上時，線段PM、PN、AD的數量關系是 ．
（2）類比探究
如圖2，若α=90°，P在線段BC上時，判斷線段PM、PN、AD的數量關系，并說明理由．
（3）問題解決
若α=120°，點P在線段BC兩端點的外端，且AD=2，請直接寫出PM-PN的值．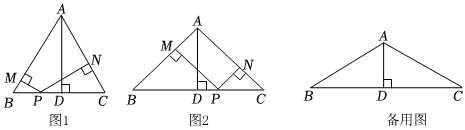
發布：2025/5/24 20:0:2組卷：74引用：1難度：0.3