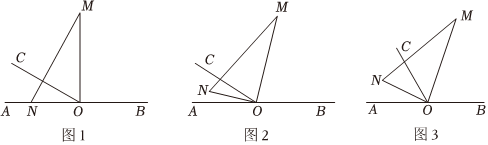
如圖，O為直線AB上一點，過點O作射線OC，∠AOC=30°，將一直角三角板（∠M=30°）的直角頂點放在點O處，一邊ON在射線OA上，另一邊OM與OC都在直線AB的上方．
（1）將圖1中的三角板繞點O以每秒3°的速度沿順時針方向旋轉一周．如圖，經過t秒后，OM恰好平分∠BOC．求t的值；并判斷此時ON是否平分∠AOC？請說明理由；
（2）在（1）問的基礎上，若三角板在轉動的同時，射線OC也繞O點以每秒6°的速度沿順時針方向旋轉一周，如圖，那么經過多長時間OC平分∠MON？請說明理由．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/23 8:0:8組卷：2857引用：4難度：0.3
相似題
-
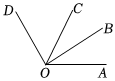1．如圖，∠AOD=120°，OC平分∠AOD，OB平分∠AOC，下列結論：①∠AOC=∠COD；②∠COD=2∠BOC；③∠AOB與∠COD可以拼成一個直角；④∠AOC與∠AOD可以拼成一個平角，正確的個數有（ ）發布：2025/6/7 16:30:2組卷：39引用：1難度：0.7 -
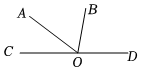2．如圖所示，已知點O是直線CD上的一點，∠AOC=30°，OB平分∠AOD，則∠BOD的度數是（ ）發布：2025/6/7 20:30:1組卷：510引用：5難度：0.4 -
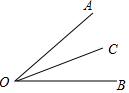3．如圖，OC為∠AOB內的一條射線，下列條件中不能確定OC平分∠AOB的是（ ）發布：2025/6/7 4:0:1組卷：582引用：3難度：0.7