已知拋物線y=ax2+kx+h（a＞0）．
（1）通過配方可以將其化成頂點式為 y=a（x+k2a）2+4ah-k24ay=a（x+k2a）2+4ah-k24a，根據(jù)該拋物線在對稱軸兩側(cè)從左到右圖象的特征，可以判斷，當頂點在x軸 下方下方（填上方或下方），即4ah-k2＜＜0（填大于或小于）時，該拋物線與x軸必有兩個交點；
（2）若拋物線上存在兩點A（x1，y1），B（x2，y2），分布在x軸的兩側(cè)，則拋物線頂點必在x軸下方，請你結(jié)合A、B兩點在拋物線上的可能位置，根據(jù)二次函數(shù)的性質(zhì)，對這個結(jié)論的正確性給以說明；（為了便于說明，不妨設x1＜x2且都不等于頂點的橫坐標；另如果需要借助圖象輔助說明，可自己畫出簡單示意圖）
（3）利用二次函數(shù)（1）（2）結(jié)論，求證：當a＞0，（a+c）（a+b+c）＜0時，（b-c）2＞4a（a+b+c）．
y
=
a
（
x
+
k
2
a
）
2
+
4
ah
-
k
2
4
a
y
=
a
（
x
+
k
2
a
）
2
+
4
ah
-
k
2
4
a
【答案】；下方；＜
y
=
a
（
x
+
k
2
a
）
2
+
4
ah
-
k
2
4
a
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/5/25 23:30:1組卷：689引用：3難度：0.6
相似題
-
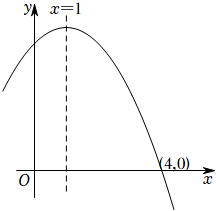1．二次函數(shù)y=ax2+bx+c（a≠0）的部分圖象如圖所示，圖象過點（4，0），對稱軸為直線x=1．下列結(jié)論：①2a+b=0；②15a+c＜0；③3a+2b＞0；④8a+5b+c＜0；⑤對于任意實數(shù)m,式子m（am+b）-b≤a都成立．其中結(jié)論正確的個數(shù)是（ ）發(fā)布：2025/5/26 6:30:2組卷：317引用：1難度：0.6 -
2．已知拋物線y=ax2+bx+c的對稱軸在y軸右側(cè)，該拋物線與x軸交于點A（-3，0）和點B，與y軸的負半軸交于點C，且OB=3OC．有下列結(jié)論：①
＜0；②b=3ac；③a=b+ca；④S△ABC=19（c2-c）．其中正確的有（ ）32發(fā)布：2025/5/26 7:0:2組卷：193引用：1難度：0.5 -
3．已知二次函數(shù)y=ax2+bx+c的圖象與x軸交于（x1，0），（x2，0）兩點，且滿足-1＜x1＜0，1＜x2＜2，則下列說法正確的個數(shù)是（ ）
①a+b+c＜0；②b＜0；③abc＞0；④若ax32+bx3=ax42+bx4（x3≠x4），則0＜x3+x4＜2．發(fā)布：2025/5/26 7:0:2組卷：88引用：1難度：0.5
相關(guān)試卷