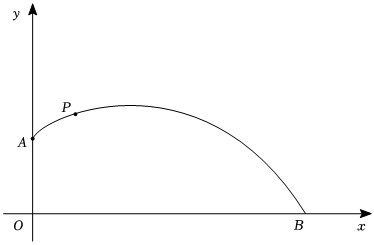
小馬同學在體育課上積極練習擲實心球，在練習過程中善于觀察的他發現，實心球擲出后在空中的軌跡是一條拋物線，每個同學擲實心球的出手高度OA是一個固定值（身高+0.65米）．如圖，小馬身高1.75米，設他拋出的實心球（記為點P）到投擲點的水平距離為x（單位：米），實心球（點P）在空中的高度為y（單位：米），y與x之間滿足的函數表達式為y=ax2+bx+c（a≠0）．
（1）c的值為 2.42.4；
（2）當a=-320時，
①若實心球落地點為B，此時b=910，求小丁本次擲實心球的水平距離OB；
②落地點要超過B，則b的取值范圍為 b＞910b＞910；
（3）已知男生擲實心球項目滿分為10.30米，小馬通過反復練習，使得自己擲出的實心球到投擲點的水平距離為4來時，恰好達到最大高度4米，你認為他能取得滿分嗎？請說明理由．
（參考數據：2≈1.41，3≈1.73，5≈2.24，6≈2.45，10≈3.16）
3
20
9
10
9
10
9
10
2
≈
3
≈
1
.
73
5
≈
2
.
24
6
≈
2
.
45
10
≈
3
.
16
【考點】二次函數的應用．
【答案】2.4；b＞
9
10
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：286引用：2難度：0.3
相似題
-
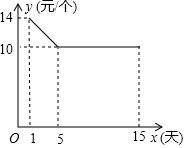1．每年九月開學前后，是文具盒的銷售旺季，商場專門設置了文具盒專柜，李經理記錄了15天的銷售數量和銷售單價，其中銷售單價y（元/個）與時間第x天（x為整數）的數量關系如圖所示，日銷量p（個）與時間第x天（x為整數）的函數關系式為：
P=20x+180（1≤x≤9）-60x+900（9≤x≤15）
（1）直接寫出y與x的函數關系式，并注明自變量x的取值范圍；
（2）設日銷售額為W（元），求W（元）關于x（天）的函數解析式；在這15天中，哪一天銷售額W（元）達到最大，最大銷售額是多少元；
（3）由于需要進貨成本和人員工資等各種開支，如果每天的營業額低于1800元，文具盒專柜將虧損，直接寫出哪幾天文具盒專柜處于虧損狀態？發布：2025/6/3 12:30:3組卷：866引用：3難度：0.4 -
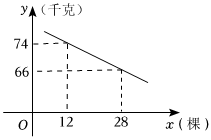2．某片果園有果樹80棵，現準備多種一些果樹提高果園產量，但是如果多種樹，那么樹之間的距離和每棵樹所受光照就會減少，單棵樹的產量隨之降低．若該果園每棵果樹產果y（千克），增種果樹x（棵），它們之間的函數關系如圖所示．
（1）求y與x之間的函數關系式．
（2）在投入成本最低的情況下，增種果樹多少棵時，果園可以收獲果實7000千克．
（3）當增種果樹多少棵時，果園的總產量w（千克）最大？此時每棵果樹的產量是多少？發布：2025/6/3 13:30:1組卷：361引用：6難度：0.5 -
3．某商店銷售一種銷售成本為每件40元的玩具，若按每件50元銷售，一個月可售出500件．銷售價每漲1元，月銷售量就減少10件．設銷售價為每件x元（x≥50），月銷量為y件，月銷售利潤為w元．
（Ⅰ）當銷售價為每件60元時，月銷量為件，月銷售利潤為元；
（Ⅱ）寫出y與x的函數解析式和w與x的函數解析式；
（Ⅲ）當銷售價定為每件多少元時會獲得最大利潤？求出最大利潤．發布：2025/6/3 10:0:1組卷：969引用：5難度：0.6