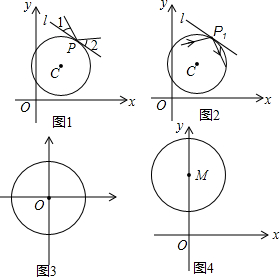
在平面直角坐標(biāo)系xOy中，過⊙C上一點P作⊙C的切線l.當(dāng)入射光線照射在點P處時，產(chǎn)生反射，且滿足：反射光線與切線l的夾角和入射光線與切線l的夾角相等，點P稱為反射點．規(guī)定：光線不能“穿過”⊙C，即當(dāng)入射光線在⊙C外時，只在圓外進行反射；當(dāng)入射光線在⊙C內(nèi)時，只在圓內(nèi)進行反射．特別地，圓的切線不能作為入射光線和反射光線．
光線在⊙C外反射的示意圖如圖1所示，其中∠1=∠2．
（1）自⊙C內(nèi)一點出發(fā)的入射光線經(jīng)⊙C第一次反射后的示意圖如圖2所示，P1是第1個反射點．請在圖2中作出光線經(jīng)⊙C第二次反射后的反射光線；
（2）當(dāng)⊙O的半徑為1時，如圖3，
①第一象限內(nèi)的一條入射光線平行于x軸，且自⊙O的外部照射在其上點P處，此光線經(jīng)⊙O反射后，反射光線與y軸平行，則反射光線與切線l的夾角為4545°；
②自點A（-1，0）出發(fā)的入射光線，在⊙O內(nèi)不斷地反射．若第1個反射點P1在第二象限，且第12個反射點P12與點A重合，則第1個反射點P1的坐標(biāo)為（-32，12）（-32，12）；
（3）如圖4，點M的坐標(biāo)為（0，2），⊙M的半徑為1．第一象限內(nèi)自點O出發(fā)的入射光線經(jīng)⊙M反射后，反射光線與坐標(biāo)軸無公共點，求反射點P的縱坐標(biāo)的取值范圍．
3
2
1
2
）
3
2
1
2
）
【考點】圓的綜合題．
【答案】45；（-，
3
2
1
2
）
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/27 12:0:9組卷：70引用：3難度：0.3
相似題
-
1．如果一個四邊形的對角線相等，我們稱這個四邊形為美好四邊形．
【問題提出】
（1）如圖①，點E是四邊形ABCD內(nèi)部一點，且滿足EB=EC，EA=ED，∠BEC=∠AED，請說明四邊形ABCD是美好四邊形；
【問題探究】
（2）如圖②，△ABC，請利用尺規(guī)作圖，在平面內(nèi)作出點D使得四邊形ABCD是美好四邊形，且滿足AD=BD．保留作圖痕跡，不寫畫法；
（3）在（2）的條件下，若圖②中△ABC滿足：∠ABC=90°，AB=4，BC=3，求四邊形ABCD的面積；
【問題解決】
（4）如圖③，某公園內(nèi)需要將4個信號塔分別建在A、B、C、D四處，現(xiàn)要求信號塔C建在公園內(nèi)一個湖泊的邊上，該湖泊可近似看成一個半徑為200m的圓，記為⊙E．已知點A到該湖泊的最近距離為500m,是否存在這樣的點D，滿足AC=BD，且使得四邊形ABCD的面積最大？若存在，求出最大值；若不存在，請說明理由．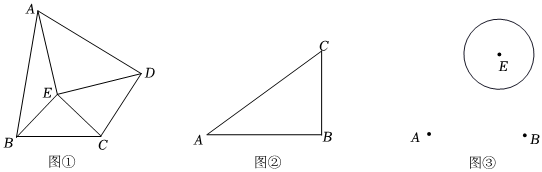
發(fā)布：2025/5/25 3:30:2組卷：216引用：2難度：0.1 -
2．【根底鞏固】
（1）如圖，在△ABC中，D為AB上一點，∠ACD=∠B．求證：AC2=AD?AB．
【嘗試應(yīng)用】
（2）如圖2，在菱形ABCD中，E，F(xiàn)分別為BC，DC上的點，且∠EAF=∠BAD，射線AE交DC的延長線于點M，射線AF交BC的延長線于點N．若AF=4，CF=2，AM=10．12
求：①CM的長；
②FN的長．
【拓展進步】
（3）如圖3，在菱形ABCD中，AB=6，∠B=60°，以點B為圓心作半徑為3的圓，其中點P是圓上的動點，請直接寫出PD+PC的最小值．12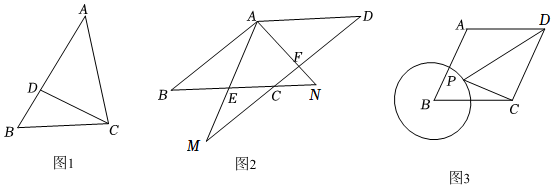
發(fā)布：2025/5/25 2:30:1組卷：870引用：2難度：0.1 -
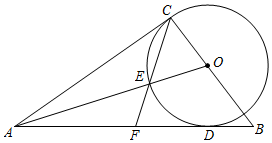3．如圖，在△ABC的邊BC上取一點O，以O(shè)為圓心，OC為半徑畫⊙O，⊙O與邊AB相切于點D，AC=AD，連接OA交⊙O于點E，連接CE，并延長交線段AB于點F．
（1）求證：AC是⊙O的切線；
（2）若AB=10，tanB=，求⊙O的半徑；43
（3）若F是AB的中點，試探究BD+CE與AF的數(shù)量關(guān)系并說明理由．發(fā)布：2025/5/25 3:0:2組卷：6113引用：25難度：0.2