【閱讀理解】
在一個三角形中，如果有兩個內角α與β滿足2α+β=90°，那么我們稱這樣的三角形為“亞直角三角形”．根據這個定義，顯然α+β＜90°，則這個三角形的第三個角為180°-（α+β）＞90°，這就是說“亞直角三角形”是特殊的鈍角三角形．
【嘗試運用】
（1）若某三角形是“亞直角三角形”，且一個內角為100°，請直接寫出它的兩個銳角的度數；
（2）如圖1，在Rt△ABC中，∠ACB=90°，AC=6，BC=9，點D在邊BC上，連接AD，且AD不平分∠BAC．若△ABD是“亞直角三角形”，求線段AD的長；
【素養提升】
（3）如圖2，在鈍角△ABC中，∠ABC＞90°，AB=7，BC=15，△ABC的面積為42，求證：△ABC是“亞直角三角形”．
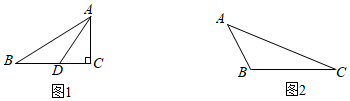
【考點】三角形綜合題．
【答案】（1）10°，70°．
（2）2．
（3）證明見解析部分．
（2）2
13
（3）證明見解析部分．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：178引用：2難度：0.1
相似題
-
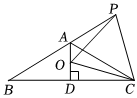1．如圖，已知△ABC中高AD恰好平分邊BC，∠B=30°，點P是BA延長線上一動點，點O是線段AD上一動點，且OP=OC，下面的結論：
①AO+AP=AB；
②OP+OC的最小值為2AB；
③∠APO+∠PCB=90°；
④S△ABC=S四邊形AOCP．
其中正確的有幾個？（ ）發布：2025/5/30 12:0:2組卷：658引用：4難度：0.3 -
2．如圖1，在△ABC中，AB=AC，BC=2，點O為△ABC兩外角∠CBD，∠BCE的平分線的交點，連接OB，OC．
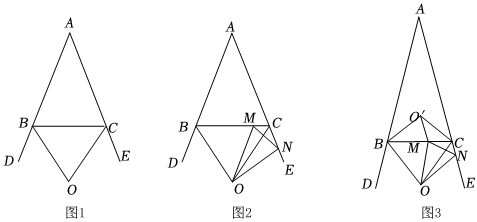
（1）求證OB=OC；
（2）如圖2，點M在線段BC上，點N為射線CE上一點，且滿足∠ABC=2∠MON．
①求△CMN的周長；
②如圖3，若∠A=30°，且點O'為∠ABC，∠ACB的平分線的交點，線段AC上是否存在一點G，使得△CGM與△CMN的周長相等？若存在，請直接寫出∠MO'G的度數；若不存在，請說明理由．發布：2025/5/30 12:0:2組卷：167引用：5難度：0.3 -
3．我們知道：角平分線上的點到角的兩邊距離相等，如圖①，E是∠AOB的平分線OP上任意一點，若EC⊥OA，ED⊥OB，垂足分別為C，D，則EC=ED．
換一種眼光看：如圖①，OP是∠AOB的平分線，C、D、E分別是OA、OB、OP上的動點，若∠OCE=∠ODE=90°，則CE=DE．
（1）一般化：如圖②，射線OP是∠AOB的平分線，C，D，E分別是OA，OB，OP上的動點，若∠OCE=∠ODE，則CE與DE的數量關系是 ．
（2）再倒過來想一想：如圖③，OP是∠AOB的平分線，C、D、E分別是OA、OB、OP上的動點，若CE=DE，則∠OCE與∠ODE有什么關系？請將圖形補充完整并結合圖形證明你的結論；
（3）用用看：已知點A（0，10）在y軸上，點B（-3，4）在函數y=-x的圖象上，點C在函數y=43x的圖象上，連接AB、AC，若AB=AC，直接寫出點C的坐標．43發布：2025/5/30 16:0:6組卷：406引用：1難度：0.3