將一張等邊三角形紙片剪成四個大小、形狀一樣的小等邊三角形(如圖所示),記為第一次操作,然后將其中右下角的等邊三角形又按同樣的方法剪成四小片,記為第二次操作,若每次都把右下角的等邊三角形按此方法剪成四小片,如此循環進行下去.
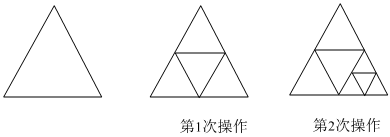
(1)如果剪n次共能得到 (3n+1)(3n+1)個等邊三角形,
(2)若原等邊三角形的邊長為1,設an表示第n次所剪出的小等邊三角形的邊長,如a1=12;
①試用含n的式子表示an=12n12n;
②計算a1+a2+a3+...+an=1-12n1-12n;
(3)運用(2)的結論,計算13+16+112+124+148+196+1192+1384+1768的值.
1
2
1
2
n
1
2
n
1
2
n
1
2
n
1
3
1
6
1
12
1
24
1
48
1
96
1
192
1
384
1
768
【考點】規律型:圖形的變化類;列代數式.
【答案】(3n+1);;1-
1
2
n
1
2
n
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/10/11 21:0:3組卷:553引用:5難度:0.5
相似題
-
1.用相同的菱形按如圖的方式搭圖形.
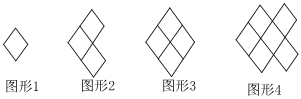
(1)按圖示規律完成下表:
(2)按這種方式搭下去,搭第2n+1(n為自然數)個圖形需要 個菱形;(用含n的式子表示)圖形 1 2 3 4 5 6 … 所用菱形個數 1 3 4 6 …
(3)小亮同學說他按這種方式搭出來的一個圖形用了2023個菱形,你認為可能嗎?如果能那是第幾個圖形?如果不可能請說明理由.發布:2025/5/23 15:0:2組卷:218引用:4難度:0.5 -
2.用正方形按如圖所示的規律拼圖案,其中第①個圖案中有5個正方形,第②個圖案中有9個正方形,第③個圖案中有13個正方形,第④個圖案中有17個正方形,此規律排列下去,則第⑩個圖案中正方形的個數為( )

A.41 B.37 C.33 D.32 發布:2025/5/23 15:0:2組卷:96引用:2難度:0.7 -
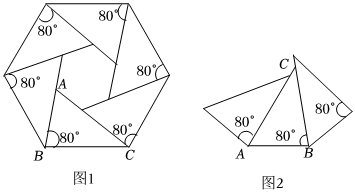 3.小明同學用一些完全相同的△ABC紙片,已知六個△ABC紙片按照圖1所示的方法拼接可得外輪廓是正六邊形圖案,若用n個△ABC紙片按圖2所示的方法拼接,那么可以得到外輪廓的圖案是( )
3.小明同學用一些完全相同的△ABC紙片,已知六個△ABC紙片按照圖1所示的方法拼接可得外輪廓是正六邊形圖案,若用n個△ABC紙片按圖2所示的方法拼接,那么可以得到外輪廓的圖案是( )A.正十二邊形 B.正十邊形 C.正九邊形 D.正八邊形 發布:2025/5/23 17:30:1組卷:125引用:2難度:0.7


