如圖，已知矩形ABCD，AB=6cm,BC=8cm,點F為CD中點．點P從點D出發，沿DA方向勻速向點A運動，同時，點E從點C出發，沿CA方向勻速向點A運動，點P，點E的運動速度均為1cm/s；當點P、E中有一點停止運動時，另一點也停止運動．連接PE、PF．設運動時間為t（s）（0＜t＜8），解答下列問題：
（1）當點P在∠ABD的平分線上時，求t的值；
（2）設△PEF的面積為y（cm2），求y與t之間的函數關系式；
（3）連接DE，在運動過程中，是否存在某一時刻t,使得△CDE是等腰三角形．若存在，求出t的值；若不存在，請說明理由．
【考點】四邊形綜合題．
【答案】（1）當點P在∠ABD的平分線上時，求t的值；
（2）y=-0.3t2+2.7t；
（3）t的值是5或6或7.2．
（2）y=-0.3t2+2.7t；
（3）t的值是5或6或7.2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/21 8:0:10組卷：415引用：2難度：0.1
相似題
-
1．如圖1，菱形ABCD中，∠A=120°，AB=4，點P在CD上，連接BP，將△BCP沿BP翻折，得到△BMP，連接CM，延長CM交AD于點E．
（1）當點P從點C運動到點D時，AE的長隨之變化，請寫出AE長的取值范圍：．
（2）在圖2中，當MP⊥CD時，求證：BM平分∠ABC．
（3）當點P在CD上移動過程中，是否存在CP=AE的情況？如果存在，求此時CP的長；如果不存在，說明理由．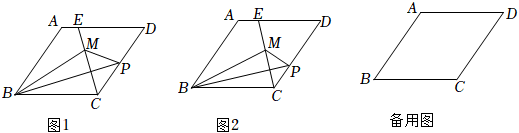
發布：2025/5/25 10:0:1組卷：79引用：1難度：0.1 -
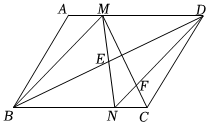2．如圖，在平行四邊形ABCD中，E是BD的中點，則下列四個結論：
（1）AM=CN；
（2）若MD=AM，∠A=90°，則BM=CM；
（3）若MD=2AM，則S△MNC=S△BNE；
（4）若AB=MN，則△MFN與△DFC全等．
其中正確結論的序號為發布：2025/5/25 10:0:1組卷：86引用：2難度：0.3 -
3．【問題探究】
（1）如圖①，在四邊形ABCD中，∠B=∠D=90°，∠DAB=135°，且AB=2，AD=4．若點P是BC邊上任意一點，且∠APD=45°，求BP的長；2
【問題解決】
（2）如圖②，直角△ABC是一個公園的平面示意圖，∠B=90°，∠A=60°，AB=200m,為了人們能更好的放松娛樂，現要擴大公園使其成為一個四邊形ABCD，根據設計要求，需使△ACD為等腰三角形，且AC=BD，是否可以建一個滿足要求的面積最大的四邊形公園ABCD？若可以，求出滿足要求的四邊形ABCD的最大面積；若不可以，請說明理由．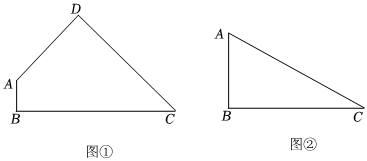
發布：2025/5/25 10:30:1組卷：46引用：1難度：0.3