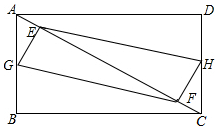
在矩形ABCD中，AB=3cm,BC=4cm,E，F是對角線AC上的兩個動點，分別從A，C同時出發相向而行，速度均為1cm/s,運動時間為t秒，當其中一個動點到達后就停止運動．
（1）若G，H分別是AB，DC中點，求證：四邊形EGFH始終是平行四邊形．
（2）在（1）條件下，當t為何值時，四邊形EGFH為矩形．
（3）若G，H分別是折線A-B-C，C-D-A上的動點，與E，F相同的速度同時出發，當t為何值時，四邊形EGFH為菱形．
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/5 8:0:9組卷：1049引用：10難度：0.1
相似題
-
1．如圖，矩形ABCD中，AB=4，BC=a（a＞4），點E在邊BC上，在AB同側以AE為邊作正方形AEFG，直線FG交直線AD于點H．
（1）如圖①，若點F是CD的中點，求a的值；
（2）如圖②，若點F在矩形ABCD內，且GH：FH=3：1，求BE的長；
（3）連接DF，若a=8，DF=2，直接寫出GH：FH的值．發布：2025/5/29 21:0:2組卷：428引用：1難度：0.3 -
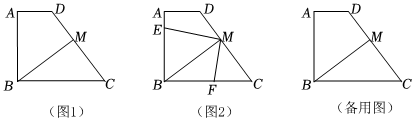
2．如圖1，梯形ABCD中，AD∥BC，∠A=90°，AD=2，AB=4，BC=5，M在邊CD上，連接BM，BM⊥DC．
（1）求CD的長；
（2）如圖2，作∠EMF=90°，ME交AB于點E，MF交BC于點F，若AE=x,BF=y,求y關于x的函數解析式，并寫出定義域；
（3）在（2）的條件下，若△MCF是等腰三角形，求AE的值．發布：2025/5/29 21:30:2組卷：141引用：2難度：0.3 -
3．【問題解決】
在一節數學課上，張老師提出了這樣一個問題：如圖1，點E是正方形ABCD內一點，BE=2，EC=4，DE=6．你能求出∠BEC的度數嗎？
小明通過觀察、分析、思考，形成了如下思路：
思路一：將△BEC繞點C逆時針旋轉90°，得到△DE'C，連接EE'，求出∠BEC的度數；
思路二：將△DEC繞點C順時針旋轉90°，得到△BE'C，連接EE'，求出∠BEC的度數．
（1）請參考小明的思路，寫出兩種思路的完整解答過程．
【類比探究】
（2）如圖2，若點E是正方形ABCD外一點，EB=8，EC=2，DE=6，求∠BEC的度數．2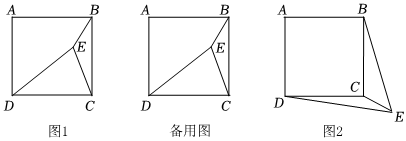
發布：2025/5/29 23:30:1組卷：197引用：4難度：0.3