閱讀材料:
如圖,小明為測量河流寬度,在河岸的一側選定點B,河的對岸垂直于河岸的方向選定觀測目標點A.小明沿點B所在河岸水平向右選取任意點P,繼續前行至與BP距離相等處選取點C,再沿與河岸垂直方向行走至點D,使得點D、P、A在同一直線時,測量CD的長即為河流的寬度.
分析:該問題也可以理解為根據BP=CP,即P為BC的中點,過點C作CD∥AB交AP于點D,從而構造了△CDP與△BAP全等,這樣的思想是抓住線段的中點,再過線段的一端作平行線,利用平行構造三角形全等,從而解決線段相等問題,也稱構造“X”型全等.
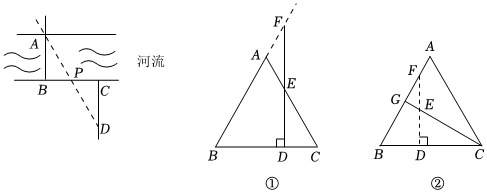
請運用以上模型思想解決以下問題:
等邊三角形ABC中,AB=4,點D在BC邊上,過點D作DF⊥BC,交射線BA于點F,則
(1)如圖①,若DF與AC相交于點E,當EF=ED時,AF與CD有什么數量關系?請說明理由;
(2)如圖②,點G是AB邊上的中點,連接CG,交DF于點E,EF=ED,求CD的長.
【答案】(1)AF=CD,理由見解析;
(2)CD=.
(2)CD=
12
5
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/6 8:0:9組卷:150引用:2難度:0.4
相似題
-
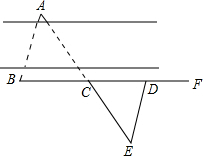 1.如圖,小明和小華兩家位于A,B兩處,隔河相望.要測得兩家之間的距離,小明設計如下方案:從點B出發沿河岸畫一條射線BF,在BF上截取BC=CD,過點D作DE∥AB,取點E使E,C,A在同一條直線上,則DE的長就是A,B之間的距離,說明他設計的道理.發布:2025/5/30 14:0:1組卷:204引用:3難度:0.7
1.如圖,小明和小華兩家位于A,B兩處,隔河相望.要測得兩家之間的距離,小明設計如下方案:從點B出發沿河岸畫一條射線BF,在BF上截取BC=CD,過點D作DE∥AB,取點E使E,C,A在同一條直線上,則DE的長就是A,B之間的距離,說明他設計的道理.發布:2025/5/30 14:0:1組卷:204引用:3難度:0.7 -
 2.如圖,一塊三角形玻璃裂成①②兩塊,現需配一塊同樣的玻璃,為方便起見,只需帶上碎片即可.發布:2025/5/30 12:30:2組卷:508引用:5難度:0.5
2.如圖,一塊三角形玻璃裂成①②兩塊,現需配一塊同樣的玻璃,為方便起見,只需帶上碎片即可.發布:2025/5/30 12:30:2組卷:508引用:5難度:0.5 -
 3.小明在物理課上學習了發聲物體的振動實驗后,對其作了進一步的探究:在一個支架的橫桿點O處用一根細繩懸掛一個小球A,小球A可以自由擺動,如圖,OA表示小球靜止時的位置.當小明用發聲物體靠進小球時,小球從OA擺到OB位置,此時過點B作BD⊥OA于點D,當小球擺到OC位置時,OB與OC恰好垂直(圖中的A、B、O、C在同一平面上),過點C作CE⊥OA于點E,測得CE=15cm,AD=2cm.
3.小明在物理課上學習了發聲物體的振動實驗后,對其作了進一步的探究:在一個支架的橫桿點O處用一根細繩懸掛一個小球A,小球A可以自由擺動,如圖,OA表示小球靜止時的位置.當小明用發聲物體靠進小球時,小球從OA擺到OB位置,此時過點B作BD⊥OA于點D,當小球擺到OC位置時,OB與OC恰好垂直(圖中的A、B、O、C在同一平面上),過點C作CE⊥OA于點E,測得CE=15cm,AD=2cm.
(1)試說明OE=BD;
(2)求DE的長.發布:2025/5/30 11:0:1組卷:368引用:1難度:0.4


