2020-2021學年貴州省遵義市紅花崗區八年級（上）期末數學試卷
發布：2024/7/6 8:0:9
一、選擇題（本題共12小題，每小題4分，共48分，在每小題給出的四個選項中，只有一項是符合題目要求的，請用2B鉛筆把答題卡上對應題目的答案標號涂黑、涂滿）
-
1．下列文字中，是軸對稱圖形的是（ ）
組卷：174引用：3難度：0.9 -
2．新型冠狀病毒屬于β屬的新型冠狀病毒，顆粒呈圓形或者橢圓形，直徑約60～140納米（1納米=10-9米），某新冠病毒的直徑大小是126納米，用科學記數法可以表示為（ ）
組卷：6引用：1難度：0.8 -
3．等腰三角形的兩邊長為2cm,5cm,則該等腰三角形的周長為（ ）
組卷：26引用：2難度：0.6 -
4．下列各式運算正確的是（ ）
組卷：11引用：2難度：0.7 -
5．點A（-2，3）向右平移3個單位后得到點B，那么點B關于x軸對稱的點的坐標是（ ）
組卷：7引用：3難度：0.8 -
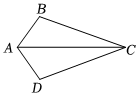6．如圖，在△ABC與△ADC中，若∠BAC=∠DAC，則下列條件不能判定△ABC與△ADC全等的是（ ）組卷：11引用：1難度：0.7 -
7．已知（x+m）（x-2）=x2-x-2，那么m的值是（ ）
組卷：9引用：1難度：0.7 -
8．如圖，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于點D，若AB=20，△ABD的面積為60，則CD長（ ）組卷：462引用：3難度：0.7
三、解答題（本題共8小題，共86分．答題請用0.5毫米黑色墨水簽字筆或鋼筆書寫在答題卡的相應位置上，解答是應寫出必要的文字說明，證明過程或演算步驟．）
-
23．閱讀材料：
如圖，小明為測量河流寬度，在河岸的一側選定點B，河的對岸垂直于河岸的方向選定觀測目標點A．小明沿點B所在河岸水平向右選取任意點P，繼續前行至與BP距離相等處選取點C，再沿與河岸垂直方向行走至點D，使得點D、P、A在同一直線時，測量CD的長即為河流的寬度．
分析：該問題也可以理解為根據BP=CP，即P為BC的中點，過點C作CD∥AB交AP于點D，從而構造了△CDP與△BAP全等，這樣的思想是抓住線段的中點，再過線段的一端作平行線，利用平行構造三角形全等，從而解決線段相等問題，也稱構造“X”型全等．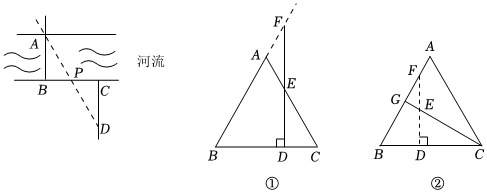
請運用以上模型思想解決以下問題：
等邊三角形ABC中，AB=4，點D在BC邊上，過點D作DF⊥BC，交射線BA于點F，則
（1）如圖①，若DF與AC相交于點E，當EF=ED時，AF與CD有什么數量關系？請說明理由；
（2）如圖②，點G是AB邊上的中點，連接CG，交DF于點E，EF=ED，求CD的長．組卷：150引用：2難度：0.4 -
24．如圖1，四邊形ABED中，∠B=∠E=∠ACD=90°，BC=DE．
（1）求證：△ABC≌△CED．
（2）發現：若AB=a,BC=b,AC=c,請用兩種方法計算四邊形ABCD的面積，并探究a、b、c之間有什么數量關系？
（3）應用：
①根據（2）中的發現，當AB=8，BC=6時，AC的長為 ；
②如圖2，若∠P=30°，PM=4，PN=7，點F在PN上，點G在射線PM上連接FM、FG、NG，求MF+FG+GN的最小值．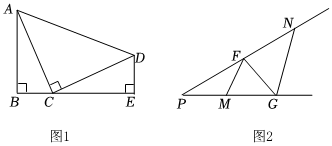
組卷：25引用：2難度：0.1