[閱讀理解]“整體思想”是一種重要的數(shù)學(xué)思想方法，在多項式的化簡求值中應(yīng)用極為廣泛．比如，4x-2x+x=（4-2+1）x=3x,類似地，我們把（a-b）看成一個整體，則4（a-b）-2（a-b）+（a-b）=（4-2+1）（a-b）=3（a-b）．
[嘗試應(yīng)用]（1）化簡4（a+b）+2（a+b）-3（a+b）的結(jié)果是 3（a+b）3（a+b）；
（2）化簡求值：6（x+y）2+5（x+y）-2（x+y）-3（x+y）2，其中x+y=1；
[拓展探索]（3）若x2-2y=4，請求出-3x2+6y+10的值．
【考點】整式的加減—化簡求值；數(shù)學(xué)常識．
【答案】3（a+b）
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：86引用：1難度：0.7
相似題
-
1．先化簡，再求值：
x-2（x-12y2）+（-13x+32y2），其中x=-2，y=13．23發(fā)布：2025/6/4 11:30:1組卷：9646引用：106難度：0.7 -
2．先化簡，再求值
（4a2b-3ab）+（-5a2b+2ab）-（2ba2-1），其中a=2，b=．12發(fā)布：2025/6/4 4:0:2組卷：1952引用：9難度：0.8 -
3．【知識回顧】題目：代數(shù)式ax-y+6+3x-5y-1的值與x的取值無關(guān)，求a的值．
解題方法：把x、y看作字母，a看作系數(shù)，合并同類項．
因為代數(shù)式的值與x的取值無關(guān)，所以含x項的系數(shù)為0．
具體解題過程：原式=（a+3）x-6y+5，
∵代數(shù)式的值與x的取值無關(guān)，
∴a+3=0，解得a=-3．
【理解應(yīng)用】
（1）若關(guān)于x的多項式m（2x-3）+2m2-4x的值與x的取值無關(guān)，求m的值；
（2）已知A=（2x+1）（x-2）-x（1-3m），B=-x2+mx-1，且A+2B的值與x的取值無關(guān)，求m的值；
【能力提升】
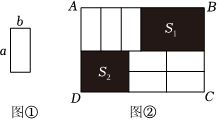
（3）7張如圖①所示的小長方形，長為a,寬為b,按照圖②所示的方式不重疊地放在大長方形ABCD內(nèi)，大長方形中未被覆蓋的兩個部分都是長方形，設(shè)右上角長方形的面積為S1，左下角長方形的面積為S2，當(dāng)AB的長變化時，S1-S2的值始終保持不變，求a與b的等量關(guān)系．發(fā)布：2025/6/4 0:0:8組卷：156引用：1難度：0.6