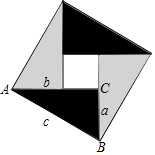
 中國古代數學家們對于勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位,體現了數學研究中的繼承和發展.現用4個全等的直角三角形拼成如圖所示“弦圖”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,請你利用這個圖形解決下列問題:
中國古代數學家們對于勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位,體現了數學研究中的繼承和發展.現用4個全等的直角三角形拼成如圖所示“弦圖”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,請你利用這個圖形解決下列問題:
(1)試說明a2+b2=c2;
(2)如果大正方形的面積是10,小正方形的面積是2,求(a+b)2的值.
【考點】勾股定理的證明.
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/14 7:0:10組卷:2680引用:13難度:0.5
相似題
-
1.在學習勾股定理的過程中,我們已經學會了運用如圖圖形,驗證著名的勾股定理,這種根據圖形直觀推論或驗證數學規律和公式的方法,簡稱為“無字證明”.實際上它也可用于驗證數與代數、圖形與幾何等領域中的許多數學公式和規律,它體現的數學思想是( )
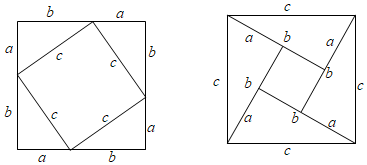
A.分類思想 B.類比思想 C.統計思想 D.數形結合思想 發布:2025/6/9 0:30:2組卷:46引用:2難度:0.6 -
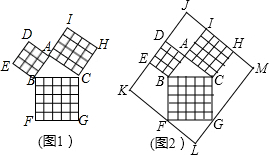 2.勾股定理在平面幾何中有著不可替代的重要地位,在我國古算書《周髀算經》中就有“若勾三,股四,則弦五”的記載.如圖1是由邊長均為1的小正方形和Rt△ABC構成的,可以用其面積關系驗證勾股定理.將圖1按圖2所示“嵌入”長方形LMJK,則該長方形的面積為( )
2.勾股定理在平面幾何中有著不可替代的重要地位,在我國古算書《周髀算經》中就有“若勾三,股四,則弦五”的記載.如圖1是由邊長均為1的小正方形和Rt△ABC構成的,可以用其面積關系驗證勾股定理.將圖1按圖2所示“嵌入”長方形LMJK,則該長方形的面積為( )A.120 B.110 C.100 D.90 發布:2025/6/8 3:0:2組卷:1952引用:7難度:0.5 -
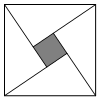 3.如圖,由四個直角邊分別為8和6的全等直角三角形拼成“趙爽弦圖”,其中陰影部分面積為.發布:2025/6/9 0:0:2組卷:788引用:11難度:0.7
3.如圖,由四個直角邊分別為8和6的全等直角三角形拼成“趙爽弦圖”,其中陰影部分面積為.發布:2025/6/9 0:0:2組卷:788引用:11難度:0.7


