“以形釋數(shù)”是利用數(shù)形結(jié)合思想證明代數(shù)問題的一種體現(xiàn),做整式的乘法運(yùn)算時(shí)利用幾何直觀的方法獲取結(jié)論,在解決整式運(yùn)算問題時(shí)經(jīng)常運(yùn)用.
例1:如圖1,可得等式:a(b+c)=ab+ac;
例2:由圖2,可得等式:(a+2b)(a+b)=a2+3ab+2b2.

(1)如圖3,將幾個(gè)面積不等的小正方形與小長方形拼成一個(gè)邊長為a+b+c的正方形,從中你發(fā)現(xiàn)的結(jié)論用等式表示為 (a+b+c)2=a2+b2+c2+2ab+2bc+2ac(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)利用(1)中所得到的結(jié)論,解決下面的問題:已知a+b+c=10,a2+b2+c2=36.求ab+bc+ac的值.
(3)如圖4,拼成AMGN為大長方形,記長方形ABCD的面積與長方形EFGH的面積差為S.設(shè)CD=x,若S的值與CD無關(guān),求a與b之間的數(shù)量關(guān)系.
【答案】(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/7/1 8:0:9組卷:2344引用:17難度:0.6
相似題
-
1.閱讀材料:利用公式法,可以將一些形如ax2+bx+c(a≠0)的多項(xiàng)式變形為a(x+m)2+n的形式,我們把這樣的變形方法叫做多項(xiàng)式ax2+bx+c(a≠0)的配方法,運(yùn)用多項(xiàng)式的配方法及平方差公式能對(duì)一些多項(xiàng)式進(jìn)行因式分解.
例如:.x2+4x-5=x2+4x+(42)2-(42)2-5=(x+42)2-4-5=(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1)
根據(jù)以上材料,解答下列問題.
(1)分解因式:x2+2x-3;
(2)求多項(xiàng)式x2+6x-9的最小值;
(3)已知a,b,c是△ABC的三邊長,且滿足a2+b2+c2+50=6a+8b+10c,求△ABC的周長.發(fā)布:2025/6/8 15:30:1組卷:2750引用:10難度:0.3 -
2.若x+y=3,xy=-4,則x2y+xy2=.
發(fā)布:2025/6/8 14:30:2組卷:148引用:3難度:0.7 -
3.數(shù)形結(jié)合思想是根據(jù)數(shù)與形之間的對(duì)應(yīng)關(guān)系,通過數(shù)與形的相互轉(zhuǎn)化來解決數(shù)學(xué)問題的思想.我們常利用數(shù)形結(jié)合思想,借助形的幾何直觀性來闡明數(shù)之間某種關(guān)系,如:探索整式乘法的一些法則和公式.
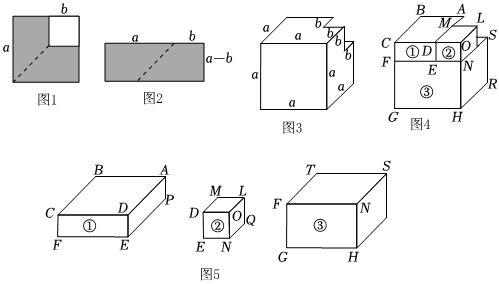
(1)探究一:
將圖1的陰影部分沿虛線剪開后,拼成圖2的形狀,拼圖前后圖形的面積不變,因此可得一個(gè)多項(xiàng)式的分解因式 .
(2)探究二:類似地,我們可以借助一個(gè)棱長為a的大正方體進(jìn)行以下探索:
在大正方體一角截去一個(gè)棱長為b(b<a)的小正方體,如圖3所示,則得到的幾何體的體積為 ;
(3)將圖3中的幾何體分割成三個(gè)長方體①、②、③,如圖4、圖5所示,∵BC=a,AB=a-b,CF=b,∴長方體①的體積為ab(a-b).類似地,長方體②的體積為 ,長方體③的體積為 ;(結(jié)果不需要化簡(jiǎn))
(4)用不同的方法表示圖3中幾何體的體積,可以得到的恒等式(將一個(gè)多項(xiàng)式因式分解)為 .
(5)問題應(yīng)用:利用上面的結(jié)論,解決問題:已知a-b=6,ab=2,求a3-b3的值.
(6)類比以上探究,嘗試因式分解:a3+b3=.發(fā)布:2025/6/8 15:0:1組卷:433引用:4難度:0.6


