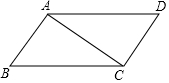
如圖，已知四邊形ABCD是平行四邊形，∠B是銳角，AC是對角線．
（1）作∠AEB=∠B，且點E在BC上，并連接DE（要求：尺規作圖，保留作圖痕跡，不寫作法）；
（2）在（1）的條件下，求證：AC=DE．
【答案】（1）作圖見解析部分．
（2）證明見解析部分．
（2）證明見解析部分．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/9 17:30:1組卷：83引用：2難度：0.5
相似題
-
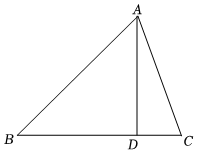1．如圖所示，等腰△ABC，BA=BC，AD⊥BC．
（1）過點B作∠ABD的平分線交AD于點E（要求：保留作圖痕跡，不寫作法）；
（2）在（1）的條件下，已知AD=BD，求證：BE=AC．發布：2025/6/9 18:30:1組卷：331引用：8難度：0.7 -
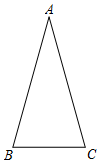2．如圖，在△ABC中，AB=AC．
（1）利用尺規作圖作邊BC的高AD，垂足為D（保留作圖痕跡，不寫作法）；
（2）求證：BD=CD．
（3）如果三角形的周長是22，一邊長為5，求它的另外兩邊長．發布：2025/6/9 22:0:2組卷：40引用：2難度：0.4 -
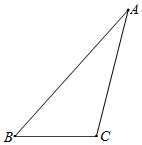3．下面是小明設計的“作三角形的高線”的尺規作圖過程．
已知：△ABC．
求作：BC邊上的高線．
作法：如圖，
①以點C為圓心，CA為半徑畫弧；
②以點B為圓心，BA為半徑畫弧，兩弧相交于點D；
③連接AD，交BC的延長線于點E．
所以線段AE就是所求作的BC邊上的高線．
根據小明設計的尺規作圖過程，
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面證明．
證明：∵CA=CD，
∴點C在線段AD的垂直平分線上（填推理的依據）．
∵=，
∴點B在線段AD的垂直平分線上．
∴BC是線段AD的垂直平分線．
∴AD⊥BC．
∴AE就是BC邊上的高線．發布：2025/6/9 22:0:2組卷：121引用：4難度：0.8