如圖中，圖（1）是一個菱形ABCD，將其作如下劃分：
第一次劃分：如圖（2）所示，連接菱形ABCD對邊中點，共得到5個菱形；
第二次劃分：如圖（3）所示，對菱形CEFG按上述劃分方式繼續劃分，共得到9個菱形；
第三次劃分：如圖（4）所示，…
依次劃分下去．
（1）根據題意，第四次劃分共得到 1717個菱形，第n次劃分共得到 （1+4n）（1+4n）個菱形；
（2）根據（1）的規律，請你按上述劃分方式，判斷能否得到2023個菱形？為什么？
【考點】規律型：圖形的變化類．
【答案】17；（1+4n）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/4 8:30:1組卷：214引用：3難度：0.7
相似題
-
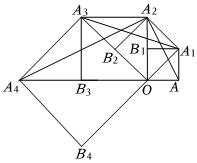1．如圖，四邊形OAA1B1是邊長為1的正方形，以對角線OA1為邊作第二個正方形OA1A2B2，連接AA2，得到△AA1A2；再以對角線OA2為邊作第三個正方形OA2A3B3連接A1A3，得到△A1A2A3；再以對角線OA3為邊作第四個正方形OA3A4B4，連接A2A4，得到△A2A3A4…．設△AA1A2，△A1A2A3，△A2A3A4，…的面積分別為S1，S2，S3，…此下去，則S2023的值為（ ）發布：2025/6/5 2:0:4組卷：47引用：1難度：0.6 -
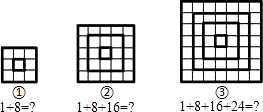2．如圖，觀察圖形及圖形所對應的算式，根據你發現的規律計算1+8+16+24+…+8n（n是正整數）的結果是．發布：2025/6/6 3:0:2組卷：259引用：9難度：0.7 -
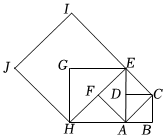3．如圖，四邊形ABCD是邊長為1的正方形，以對角線AC為邊作第二個正方形ACEF，再以對角線AE為邊作第三個正方形AEGH，如此進行下去……記正方形ABCD的邊長為a1=1，按上述方法所作的正方形的邊長依次為a2，a3，a4，……an，則an=．（用含n的式子表示）發布：2025/6/6 3:30:7組卷：25引用：4難度：0.6