（1）如圖1，∠MAN=90°，射線AD在這個角的內部，點B、C分別在∠MAN的邊AM、AN上，且AB=AC，CF⊥AD于點F，BE⊥AD于點E．求證：EF+FC=BE；
（2）如圖2，點B、C分別在∠MAN的邊AM、AN上，點E、F都在∠MAN內部的射線AD上，∠1、∠2分別是△ABE、△CAF的外角．已知AB=AC，且∠1=∠2=∠BAC，點E是AF的中點，BE=8．求FC的長；
（3）如圖3，在△ABC中，AB=AC，點D在邊BC上，點E、F在線段AD上，點E是AF的中點，∠1=∠2=∠BAC，連接EC．若△DEC的面積為4，求△BED的面積．
?
【考點】三角形綜合題．
【答案】（1）證明見解析；
（2）4；
（3）8．
（2）4；
（3）8．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/25 9:0:2組卷：36引用：1難度：0.5
相似題
-
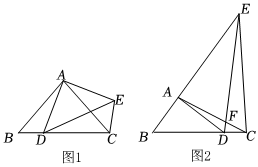1．如圖，Rt△ABC與Rt△ADE的直角頂點重合于點A，點D在BC邊上（不與B，C重合）．
（1）如圖1，當∠ABC=∠ADE=45°時，請直接寫出線段BD，CE之間的數量關系．
（2）如圖2，當∠ABC=∠ADE=60°時，設AC與DE交于點F．①求證EC=BD．②若BD=3，DC=1，試分別探求tan∠FDC和3的值．FDFC發布：2025/5/24 21:30:1組卷：21引用：1難度：0.2 -
2．性質探究
如圖（1），在等腰三角形ABC中，∠ACB=120°，則底邊AB與腰AC的長度之比為．
理解運用
（1）若頂角為120°的等腰三角形的周長為4+2，則它的面積為；3
（2）如圖（2），在四邊形EFGH中，EF=EG=EH，在邊FG，GH上分別取中點M，N，連接MN．若∠FGH=120°，EF=20，求線段MN的長．
類比拓展
頂角為2α的等腰三角形的底邊與一腰的長度之比為．（用含α的式子表示）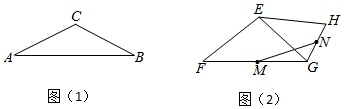
發布：2025/5/24 21:30:1組卷：815引用：4難度：0.2 -
3．問題情景：已知在△ABC中，AB=AC，∠BAC=α，過點A作AD⊥BC于點D，點P為直線BC上一點（不與點B、C重合），過點P作PM⊥AB于點M，PN⊥AC于點N．
（1）觀察猜想
如圖1，若α=60°，P在線段BC上時，線段PM、PN、AD的數量關系是 ．
（2）類比探究
如圖2，若α=90°，P在線段BC上時，判斷線段PM、PN、AD的數量關系，并說明理由．
（3）問題解決
若α=120°，點P在線段BC兩端點的外端，且AD=2，請直接寫出PM-PN的值．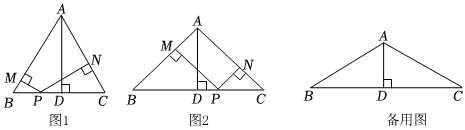
發布：2025/5/24 20:0:2組卷：74引用：1難度：0.3