綜合與實踐
綜合與實踐課上，老師讓同學們以“三角形的折疊”為主題開展數學活動．
（1）操作判斷
操作一：折疊三角形紙片，使BC與BA邊在一條直線上，得到折痕BD；
操作二：折疊三角形紙片，得到折痕AE，使B，C，E三點在一條直線上．
完成以上操作后把紙片展平，如圖1，判斷∠ABD和∠CBD的大小關系是 ∠ABD=∠CBD∠ABD=∠CBD，直線BC，AE的位置關系是 BC⊥AEBC⊥AE．
（2）深入探究
操作三：折疊三角形紙片，使點A落在折痕AE上，得到折痕DF，把紙片展平．
根據以上操作，如圖2，判斷∠DBF和∠BDF是否相等，并說明理由．
（3）結論應用
如圖1，已知∠ABC=58°，∠ACB=48°，請直接寫出∠BDC的度數．
【考點】三角形內角和定理．
【答案】∠ABD=∠CBD；BC⊥AE
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/5 8:0:9組卷：311引用：6難度：0.7
相似題
-
1．直角△ABC中，∠C=90°，點D，E分別是邊AC，BC上的點，點P是一動點，令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．
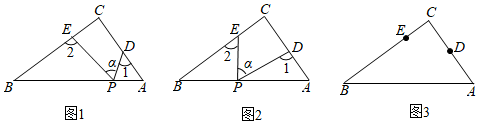
（1）若點P在線段AB上，如圖1所示，且∠α=50°，則∠1+∠2=；
（2）若點P在邊AB上運動，如圖2所示，則∠α、∠1、∠2之間有何關系，并說明理由；
（3）如圖3，若點P在斜邊BA的延長線上運動（CE＜CD），請寫出∠α、∠1、∠2之間的關系式．發布：2025/6/21 0:30:1組卷：1217引用：5難度：0.6 -
2．如圖1，△ABC中，AD平分∠BAC交BC于點D，AE⊥BC，垂足為E，CF∥AD．
（1）如圖1，∠B=30°，∠ACB=70°，求∠CFE的度數；
（2）若（1）中的∠B=α，∠ACB=β（α＜β），則∠CFE=；（用α、β表示）
（3）如圖2，（2）中的結論還成立么？請說明理由．發布：2025/6/21 0:30:1組卷：1078引用：6難度：0.6 -
3．如圖1，∠AOB=90°，點C，D分別在射線OA，OB上運動（均不與點O重合），連接CD，∠ACD的角平分線CE的反向延長線與∠CDO的角平分線DF相交于點F．
（1）若∠OCD=60°，則∠F=°；
（2）如圖1，若∠OCD=50°時，求∠F的度數；
（3）如圖2，設∠OCD的度數是2m°，則
①∠FCO=°，∠FDC=°（用含m的代數式表示）；
②∠F=°．
發布：2025/6/21 0:30:1組卷：1704引用：3難度：0.2