 問題情境
問題情境
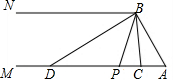
在綜合實踐課上,老師組織七年級(2)班的同學開展了探究兩角之間數(shù)量關系的數(shù)學活動,如圖,已知射線AM∥BN,連接AB,點P是射線AM上的一個動點(與點A不重合),BC,BD分別平分∠ABP和∠PBN,分別交射線AM于點C,D.
探索發(fā)現(xiàn)
“快樂小組”經(jīng)過探索后發(fā)現(xiàn):
(1)當∠A=60°時,求證:∠CBD=∠A.
(2)不斷改變∠A的度數(shù),∠CBD與∠A卻始終存在某種數(shù)量關系,
當∠A=40°,則∠CBD=7070度,
當∠A=x°時,則∠CBD=(90-x2)(90-x2)度,(用含x的代數(shù)式表示)
操作探究
(3)“智慧小組”利用量角器量出∠APB和∠ADB的度數(shù)后,探究二者之間的數(shù)量關系.他們驚奇地發(fā)現(xiàn),當點P在射線AM上運動時,無論點P在AM上的什么位置,∠APB與∠ADB之間的數(shù)量關系都保持不變,請寫出它們的關系,并說明理由.
x
2
x
2
【答案】70;(90-)
x
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/7/18 8:0:9組卷:477引用:6難度:0.5
相似題
-
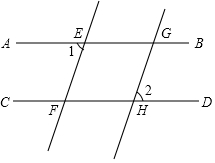 1.如圖,AB∥CD,EF∥GH,∠1=60°,則∠2補角的度數(shù)是( )
1.如圖,AB∥CD,EF∥GH,∠1=60°,則∠2補角的度數(shù)是( )A.60° B.100° C.110° D.120° 發(fā)布:2025/5/25 1:30:1組卷:719引用:7難度:0.7 -
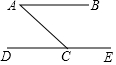 2.如圖,DE∥AB,若∠A=40°,則∠ACE=( )
2.如圖,DE∥AB,若∠A=40°,則∠ACE=( )A.40° B.140° C.80° D.120° 發(fā)布:2025/5/25 2:0:6組卷:240引用:4難度:0.7 -
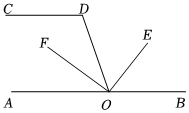 3.如圖,CD∥AB,點O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,則∠AOF=( )
3.如圖,CD∥AB,點O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,則∠AOF=( )A.25° B.30° C.35° D.40° 發(fā)布:2025/5/25 1:30:1組卷:41引用:2難度:0.5


