對任意一個四位數m,若m滿足各數位上的數字都不為0，且千位與百位上的數字不相等，十位與個位上的數字不相等，那么稱這個數為“OK數”．將一個“OK數”m的任意一個數位上的數字去掉后可以得到四個新三位數，把這四個新三位數的和與3的商記為F（m）．例如，“OK數”m=1234，去掉千位上的數字得到234，去掉百位上的數字得到134，去掉十位上的數字得到124，去掉個位上的數字得到123．這四個新三位數的和為234+134+124+123=615，615÷3=205，所以F（1234）=205．
（1）計算：F（1213），F（8567）；
（2）若“OK數”n=8900+10x+y（1≤x≤9，1≤y≤9，x,y都是正整數），F（n）也是“OK數”，且F（n）能被8整除．求F[F（n）]的值．
【考點】因式分解的應用．
【答案】（1）190，1049，
（2）198．
（2）198．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：733引用：8難度：0.4
相似題
-
1．讀下列因式分解的過程，再回答所提出的問題：
1+x+x（1+x）+x（1+x）2
=（1+x）[1+x+x（1+x）]
=（1+x）2（1+x）
=（1+x）3
（1）上述分解因式的方法是，共應用了次．
（2）若分解1+x+x（1+x）+x（1+x）2+…+x（1+x）2018，則需應用上述方法次，結果是．
（3）分解因式：1+x+x（1+x）+x（1+x）2+…+x（1+x）n發布：2025/6/22 14:0:2組卷：228引用：3難度：0.4 -
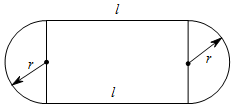2．如圖，操場的兩端為半圓形，中間是一個長方形．已知半圓的半徑為r,直跑道的長為l,請用關于r,l的多項式表示這個操場的面積．這個多項式能分解因式嗎？若能，請把它分解因式，并計算當r=40m,l=30πm時操場的面積（結果保留π）；若不能，請說明理由．發布：2025/6/22 14:30:2組卷：41引用：4難度：0.7 -
3．已知2x-y=
，xy=2，求2x4y3-x3y4的值．13發布：2025/6/22 2:0:1組卷：70引用：2難度：0.9