綜合與探究
課堂情境：數軸是規定了原點、正方向和單位長度的直線．任何有理數都可以用數軸上的點表示．數軸上表示一個數的點到原點的距離叫做這個數的絕對值．數軸上右邊的數總比左邊的數大……根據這些性質，我們可以借助數軸解決很多問題．
今天我們研究數軸上兩點之間的距離與這兩個有理數之間的關系．
觀察發現：
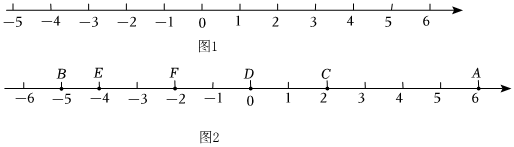
（1）填空：如圖1所示，在數軸上，有理數5與2對應的兩點之間的距離為

3

3

；
在數軸上，有理數6與-1對應的兩點之間的距離為

7

7

；
在數軸上，有理數-1與-5對應的兩點之間的距離為

4

4

；
答疑解惑：
小明提出：在數軸上，有理數-4與-1對應的兩點之間的距離可以寫為-4-（-1）嗎？
小亮回答：不可以．兩點之間的距離不能是負數．兩個點之間的距離應該寫成這兩個數的差的絕對值；
小慧回答：不可以．兩個點之間的距離等于右邊的數減去左邊的數．
方法驗證：
（2）觀察圖2數軸上給出的兩點之間距離，選用小亮或小慧的方法求數軸上兩點之間距離；
AB=

11

11

；EF=

2

2

；AC=

4

4

；DE=

4

4

；
解決問題：
（3）若點P從點A出發以每秒2個單位長度的速度向左運動，同時點Q從點B出發以每秒1個單位長度的速度向右運動，求經過多長時間P，Q兩點之間的距離為2個單位長度？