在平面直角坐標系xOy中，對于點P（x,y）和Q（x,y'）．給出如下定義：如果y′=y（x≥0） -y（x＜0）
，那么稱點Q為點P的“沉毅點”．例如點（1，2）的“沉毅點”為點（1，2），點（-1，2）的“沉毅點”為點（-1，-2）．
（1）若直線y=x+3上點M的“沉毅點”是N（n,4），求點M的坐標；
（2）若雙曲線y=kx（x＜0）上點P的“沉毅點”為點Q，且S△POQ=4，求k的值；
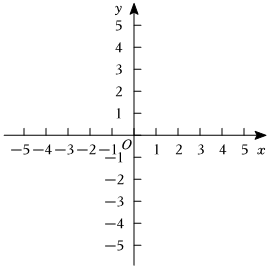
（3）若點P在函數y=-x2+4（-2≤x≤a）上，其“沉毅點”Q的縱坐標y'的取值范圍是-4＜y'≤4，結合圖象寫出a的取值范圍．
y
′
=
y （ x ≥ 0 ） |
- y （ x ＜ 0 ） |
y
=
k
x
【答案】（1）（1，4）或（-7，-4）；
（2）k=±4；
（3）2≤a＜2．
（2）k=±4；
（3）2≤a＜2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：369引用：2難度：0.5
相似題
-
1．已知點A（x1，y1），B（x2，y2）為反比例函數y=
（k≠0）圖象上的兩點，若x1=x2+1，kx=3，則k的值為．2y1-2y2發布：2025/5/23 11:30:2組卷：474引用：2難度：0.6 -
2．已知點（-3，y1），（-1，y2），（1，y3）在函數
的圖象上，那么y1，y2，y3的大小關系是 ．y=-3x發布：2025/5/23 11:0:1組卷：50引用：1難度：0.5 -
3．已知點A（x1，-2），B（x2，-1），C（x3，1）都在反比例函數y=
（k＜0）的圖象上，則x1，x2，x3的大小關系是（ ）kx發布：2025/5/23 11:30:2組卷：387引用：3難度：0.6