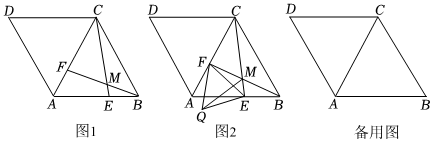
如圖，已知菱形ABCD中，∠ABC=60°，點F在射線AC上，點E在射線BA上，AF=BE，直線CE和直線BF交于點M．
（1）如圖1，當點F在線段AC上時．
①求證：△ABF≌△BCE；
②直接寫出∠BMC的度數 120120°；
（2）如圖2，點F在線段AC上時，連接EF，將線段EF繞點E按逆時針方向旋轉60°得線段EQ，連接FQ，MQ，試確定三條線段EM，FM，MQ滿足的數量關系，并證明你的猜想；
（3）若AB=47，連接DM，點N是DM的中點，連接CN，當BM=2CM時，CN的長為 6或22136或2213.（直接寫出結果）
AB
=
4
7
2
21
3
2
21
3
【考點】四邊形綜合題．
【答案】120；6或
2
21
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/14 8:0:9組卷：162引用：1難度：0.5
相似題
-
1．（1）如圖1，在四邊形ABCD中，DA=DC，∠A=∠C=90°，E、F分別是邊AB、BC上的點，且∠EDF=
∠ADC，請直接寫出圖中線段AE、EF、FC之間的數量關系 ．12
（2）如圖2，在四邊形ABCD中，DA=DC，∠A+∠C=180°，E、F分別是邊AB、BC上的點，且∠EDF=∠ADC，上述結論是否仍然成立，并說明理由．12
（3）如圖3，在四邊形ABCD中，DA=DC，∠A+∠BCD=180°，E、F分別是邊AB、BC延長線上的點，且∠EDF=∠ADC，（1）中的結論是否仍然成立？若成立，請證明；若不成立，線段AE、EF、FC之間又有怎樣的數量關系，請直接寫出你的猜想，并說明理由．12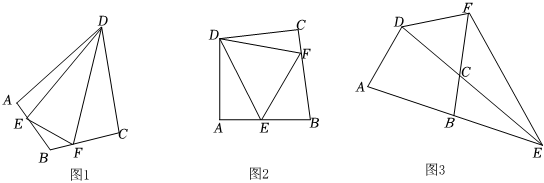
發布：2025/6/9 2:30:1組卷：165引用：1難度：0.2 -
2．下面是小明復習全等三角形時遇到的一個問題并引發的思考，請幫助小明完成以下學習任務．
如圖，OC平分∠AOB，點P在OC上，M、N分別是OA、OB上的點，OM=ON，求證：PM=PN．
小明的思考：要證明PM=PN，只需證明△POM≌△PON即可．
證法：如圖1，∵OC平分∠AOB，∴∠AOC=∠BOC，
又∵OP=OP，OM=ON，∴△MOP≌△NOP，
∴PM=PN；
請仔細閱讀并完成以下任務：
（1）小明得出△MOP≌△NOP的依據是 （填序號）．
①SSS，②SAS，③AAS，④ASA，⑤HL．
（2）如圖②，在四邊形ABCD中，AB=AD+BC，∠DAB的平分線和∠ABC的平分線交于CD邊上點P，求證：PC=PD．
（3）在（2）的條件下，如圖③，若AB=10，tan∠PAB=，當△PBC有一個內角是45°時，△PAD的面積是 ．12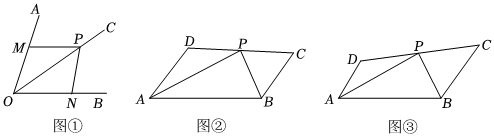
發布：2025/6/9 3:30:1組卷：114引用：3難度：0.3 -
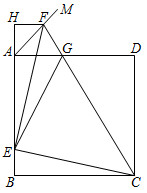3．如圖，正方形ABCD的邊長為4，點E在邊AB上，BE=1，∠DAM=45°，點F在射線AM上，且AF=，過點F作AD的平行線交BA的延長線于點H，CF與AD相交于點G，連接EC、EG，EF．下列結論：①∠EFG=45°；②△AEG的周長為8；③△CEG∽△AFG；④△CEG的面積為6.8．其中正確的個數是（ ）2發布：2025/6/9 3:0:1組卷：680引用：3難度：0.2