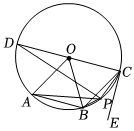
如圖，在⊙O中，CD為⊙O的直徑，過點C作射線CE，∠AOC=120°，點B為弧AC的中點，連接AB，OB，BC．點P為弧BC上的一個動點（不與B，C重合），連接PA，PB，PC，PD．
（1）若∠ECP=∠PDC，判斷射線CE與⊙O的位置關系；
（2）求證：
PA
=
3
PB
+
PC
．

【答案】（1）CE與⊙O相切，理由見解析；
（2）證明見解析．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/13 8:0:9組卷：344引用：1難度：0.3

相似題

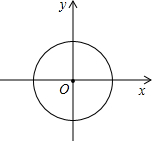1．如圖，在直角坐標系中，⊙O的半徑為1，則直線y=-x+
2
與⊙O的位置關系是（　　）
A．相離 B．相交
C．相切 D．以下三種情形都有可能
發布：2025/5/28 10:0:1組卷：343引用：24難度：0.9
解析
2．在Rt△ABC中，∠C=90°，AC=3，BC=4．若以C點為圓心，r為半徑所作的圓與斜邊AB只有一個公共點，則r的取值范圍是
．
發布：2025/5/28 17:0:2組卷：2835引用：30難度：0.5
解析
3．在Rt△ABC中，∠C=90°，AC=6，BC=8，若以C為圓心，R為半徑所作的圓與斜邊AB只有一個公共點，則R的取值范圍是

．
發布：2025/5/27 15:30:2組卷：691引用：5難度：0.7
解析

相關試卷

A．相離	B．相交
C．相切	D．以下三種情形都有可能

如圖，在⊙O中，CD為⊙O的直徑，過點C作射線CE，∠AOC=120°，點B為弧AC的中點，連接AB，OB，BC．點P為弧BC上的一個動點（不與B，C重合），連接PA，PB，PC，PD．（1）若∠ECP=∠PDC，判斷射線CE與⊙O的位置關系；（2）求證：PA=3PB+PC．