如圖1，在平面直角坐標系中，點A，B的坐標分別為A（m,0），B（n,0），且m、n滿足|m+2|+5-n=0，現同時將點A，B分別向上平移3個單位，再向右平移2個單位，分別得到點A，B的對應點C、D，連接AC，BD，CD．
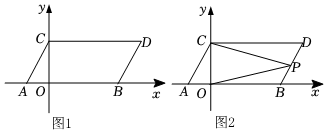
（1）直接寫出點C、D的坐標；
（2）如圖2，點P是線段BD上的一個動點，連接PC，PO，當點P在BD上移動時（不與B，D重合），∠DCP+∠BOP∠CPO的值是否發生變化？請說明理由；
（3）若點Q的坐標為（k,0），其中k＜5，且S△QOC=35S四邊形QBDC，試求出點Q的坐標．
|
m
+
2
|
+
5
-
n
=
0
∠
DCP
+
∠
BOP
∠
CPO
S
△
QOC
=
3
5
S
四邊形
QBDC
【考點】四邊形綜合題．
【答案】（1）C（0，3），B（7，3）；
（2）不變，見解析；
（3）Q的坐標為或（-18，0）．
（2）不變，見解析；
（3）Q的坐標為
（
9
2
，
0
）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：215引用：4難度：0.1
相似題
-
1．問題提出：
（1）如圖①，在Rt△ABC中，∠B=90°，AB=5，BC=12．若P是邊AC上一點，則BP的最小值為 ．
問題探究：
（2）如圖②，在Rt△ABC中，AB=BC，斜邊AC的長為，E是BC的中點，P是邊AC上一點，試求PB+PE的最小值．42
問題解決：
（3）某城區有一個五邊形MBCDP空地（∠M=∠P=∠PDC=90°，∠C=150°），城建部門計劃利用該空地建造一個居民戶外活動廣場，其中△MAB的部分規劃為觀賞區，用于種植各類鮮花，△APD部分規劃為音樂區，供老年合唱團排練合唱或廣場舞使用，四邊形ABCD部分為市民健身廣場，如圖③所示．已知AD=100米，CD=50米，∠BAD=60°，∠ABC=90°．為了進一步提升服務休閑功能，滿足市民游園和健身需求，現要在AB，AD上分別取點E，F，鋪設一條由CE，EF，FC連接而成的步行景觀道，已知鋪設景觀道的成本為100元/米，求鋪設完這條步行景觀道所需的最低成本．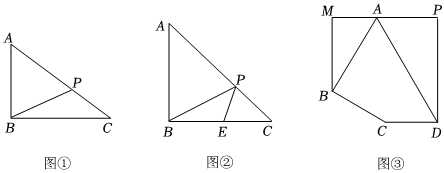
發布：2025/5/23 20:0:1組卷：771引用：5難度：0.2 -
2．綜合與實踐
（1）【操作發現】如圖1，諸葛小組將正方形紙片ABCD沿過點A的直線折疊，使點B落在正方形內部的點M處，折痕為AE，再將紙片沿過點A的直線折疊，使AD與AM重合，折痕為AF，請寫出圖中的一個45°角；
（2）【拓展探究】如圖2，孔明小組繼續將正方形紙片沿EF繼續折疊，點C的對應點恰好落在折痕AE上的點N處，連接NF交AM于點P．
①∠AEF=度；②若，求線段PM的長；AB=3
（3）【遷移應用】如圖3，在矩形ABCD中，點E，F分別在邊BC，CD上，將矩形ABCD沿AE，AF折疊，點B落在點M處，點D落在點G處，點A，M，G恰好在同一直線上，若點F為CD的三等分點，AB=3，AD=5，請直接寫出線段BE的長．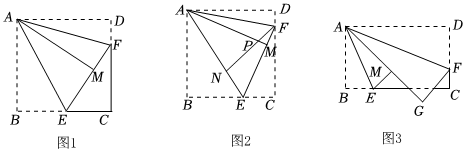
發布：2025/5/23 20:30:1組卷：1003引用：4難度：0.1 -
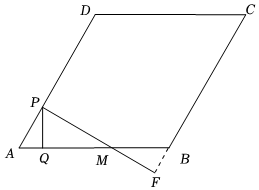3．如圖，在菱形ABCD中，AB=4，∠BAD=60°，點P從點A出發，沿線段AD以每秒1個單位長度的速度向終點D運動，過點P作PQ⊥AB于點Q，作PM⊥AD交直線AB于點M，交直線BC于點F，設△PQM與菱形ABCD重疊部分圖形的面積為S（平方單位），點P的運動時間為t（s）（0≤t≤4）．
（1）當點M與點B重合時，t=s；
（2）當t為何值時，△APQ≌△BMF；
（3）求S與t的函數關系式；
（4）以線段PQ為邊，在PQ右側作等邊△PQE，當2≤t≤4時，請直接寫出點E運動路徑的長．發布：2025/5/23 21:0:1組卷：200引用：1難度：0.1