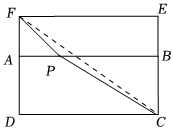
某校的數學興趣小組，探究代數式x2+12+（3-x）2+22（x＞0）的最小值．小青巧妙運用了“數形結合”的思想輕松得解．具體做法是：構造兩個有公共邊的矩形ABCD和矩形ABEF，且AB=3，BC=2，AF=1，P為AB邊上的動點，設AP=x,則PF=x2+1，PC=（3-x）2+22，問題轉化為求PC+PF的最小值．易得，P、F、C三點共線時有最小值為32．
（1）[應用]根據上面思想方法：當x=3232時，x2+22+（3-x）2+22（x＞0）有最小值．
（2）構圖求代數式x2+22+（8-x）2+62（x＞0）的最小值．
（3）[拓展]探究（x+1）2+32-x2+1（x＞0）的最大值 55（直接寫出結論）．
x
2
+
1
2
+
（
3
-
x
）
2
+
2
2
x
2
+
1
（
3
-
x
）
2
+
2
2
3
2
3
2
3
2
x
2
+
2
2
+
（
3
-
x
）
2
+
2
2
x
2
+
2
2
+
（
8
-
x
）
2
+
6
2
（
x
+
1
）
2
+
3
2
-
x
2
+
1
5
5
【考點】四邊形綜合題．
【答案】；
3
2
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：153引用：2難度：0.1
相似題
-
1．將正方形ABCD繞點A逆時針旋轉α°到正方形AEFG．
（1）如圖1，當0°＜α＜90°時，EF與CD相交于點H．求證：DH=EH；
（2）如圖2，當0°＜α＜90°，點F、D、B正好共線時，
①求∠AFB度數；
②若正方形ABCD的邊長為1，求CH的長：
（3）連接DE，EC，FC．如圖3，正方形AEFG在旋轉過程中，是否存在實數m使AE2=DE2+mFC2-EC2總成立？若存在，求m的值；若不存在，請說明理由．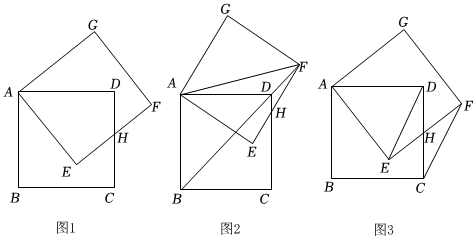
發布：2025/6/8 13:30:1組卷：67引用：1難度：0.2 -
2．定義：四邊形ABCD中，將對角線AC和BD的平方和，即AC2+BD2的值稱為四邊形ABCD的“特征數”．
（1）①在菱形ABCD中，AB=4，∠BAD=60°，則菱形ABCD的“特征數”=；
②正方形EFGH的“特征數”等于16，則邊長=；
（2）平行四邊形ABCD中，AB=a,BC=b,試證明：平行四邊形ABCD的“特征數”為2a2+2b2；
（3）利用（2）的結論解決下列問題：
平行四邊形ABCD中，，BC=6，且AC?BD=60，AC＜BD，試求AC和BD的長度．AB=42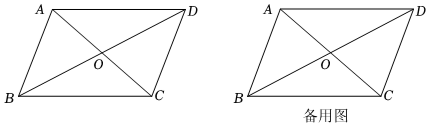
發布：2025/6/8 15:0:1組卷：373引用：3難度：0.2 -
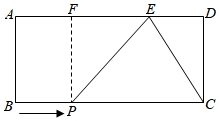3．如圖，矩形ABCD中，AB=4，AD=8，E在AD上，DE=3，點P從點B出發，以每秒1個單位長度的速度沿著BC邊向終點C運動，連接PE，設點P運動的時間為t秒．
（1）過P作PF⊥AD，垂足為F，用含t的式子表示：EF=，PC=；
（2）當t=2時，判斷△PEC是否是直角三角形，并說明理由；
（3）當∠PEC=∠DEC時，求t的值．發布：2025/6/8 12:30:1組卷：43引用：3難度：0.4