2021-2022學年廣東省珠海市香洲區紫荊中學八年級（下）期中數學試卷

一、選擇題（共10小題，每小題3分，共30分）

• 1．下列式子為最簡二次根式的是（　　）

  A． 3

  B． 4

  C． 8

  D． 1 2
  組卷：3206引用：105難度：0.9

  解析

• 2．下列計算正確的是（　　）

  A． 8 - 2 =2

  B． 2 + 3 = 5

  C． 2 × 3 =6

  D． 8 ÷ 2 =2
  組卷：22引用：1難度：0.7

  解析

• 3．以下列各組數為長度的線段，不能構成直角三角形的是（　　）

  A．2，3，4

  B．1，1， 2

  C．6，8，10

  D．5，12，13
  組卷：149引用：6難度：0.9

  解析

• 4．菱形具有而一般平行四邊形不具有的性質是（　　）

  A．對邊平行	B．對邊相等
  C．對角線互相平分	D．對角線互相垂直
  組卷：865引用：10難度：0.5

  解析

• 5．已知點（4，y₁）、（-2，y₂）在直線

  y

  =

  -

  1

  2

  x

  +

  3

  上，則y₁與y₂大小關系是（　　）

  A．y1＞y2

  B．y1=y2

  C．y1＜y2

  D．y1≤y2
  組卷：339引用：3難度：0.6

  解析

• 6．已知點D、E、F分別為△ABC各邊的中點，若△DEF的周長為24cm,則△ABC的周長為（　　）

  A．6cm

  B．12cm

  C．24cm

  D．48cm
  組卷：166引用：3難度：0.6

  解析

• 7．若正比例函數y=（a-4）x的圖象經過第一、三象限，化簡

  （

  3

  -

  a

  ）

  2

  的結果是（　　）

  A．a-3

  B．3-a

  C．（a-3）2

  D．（3-a）2
  組卷：1788引用：5難度：0.7

  解析

• 8．如圖，將一個相鄰兩邊長分別為4、8的矩形紙片ABCD折疊，使點C與點A重合，則△AEF的面積是（　　）

  A．16

  B．20

  C．10

  D．24
  組卷：72引用：1難度：0.6

  解析

五、解答題（本大題2小題，每小題10分，共20分）

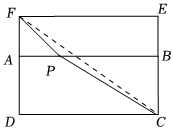• 24．某校的數學興趣小組，探究代數式

  x

  2

  +

  1

  2

  +

  （

  3

  -

  x

  ）

  2

  +

  2

  2

  （x＞0）的最小值．小青巧妙運用了“數形結合”的思想輕松得解．具體做法是：構造兩個有公共邊的矩形ABCD和矩形ABEF，且AB=3，BC=2，AF=1，P為AB邊上的動點，設AP=x,則PF=

  x

  2

  +

  1

  ，PC=

  （

  3

  -

  x

  ）

  2

  +

  2

  2

  ，問題轉化為求PC+PF的最小值．易得，P、F、C三點共線時有最小值為

  3

  2

  ．
  （1）[應用]根據上面思想方法：當x=

  時，

  x

  2

  +

  2

  2

  +

  （

  3

  -

  x

  ）

  2

  +

  2

  2

  （x＞0）有最小值．
  （2）構圖求代數式

  x

  2

  +

  2

  2

  +

  （

  8

  -

  x

  ）

  2

  +

  6

  2

  （x＞0）的最小值．
  （3）[拓展]探究

  （

  x

  +

  1

  ）

  2

  +

  3

  2

  -

  x

  2

  +

  1

  （x＞0）的最大值

  （直接寫出結論）．
  組卷：153引用：2難度：0.1

  解析

• 25．已知矩形ABCD中，AB=5，AD=4，點E在AB邊上，AE=1．點M是線段BC上的動點，BM=x,連ME，把△BME沿ME折疊，得到△FEM，延長MF交CD于點G，連接EG．
  （1）當x=

  時，△MCG是等腰三角形；
  （2）延長EG與∠CMG的平分線交于點H，連接DH，DE．
  ①在M移動過程中，四邊形DEMH能否成為菱形？若能，加以證明，并寫出此時x的值；若不能，請說明理由．
  ②在①的條件下，寫出線段DH的最小值為

  ．
  
  組卷：115引用：2難度：0.1

  解析