【閱讀理解】
排列:從n個元素中選取m(m≤n)個元素,這m個元素稱為一個排列,不同順序視作不同排列,排列數量記作Amn.
組合:從n個元素中選取m(m≤n)個元素,這m個元素稱為一個組合,不同順序視作同一組合,組合數量記作Cmn.
例如:(甲、乙),(乙、甲)是兩種不同的排列,確實同一種組合.
【問題提出1】在5個點中選取其中3個,有多少種排列?有多少種組合?
【問題解決1】
將5個點分別編號為“1”“2”“3”“4”“5”.
(一)排列:
(1)選取第1個點:
如圖①,從全部5個點中選取1個,有5種情況;
(2)選取第2個點:
如圖①,從剩余4個點中選取1個,有4種情況;
(3)選取第3個點:
如圖①,從剩余3個點中選取1個,有3種情況;
綜上所述,從5個點中任選3個點,共有5×4×3=60種排列,即A35=60.
(二)組合:
因為每個組合都包含了3個點,所有每3個點共有A33=3×2×1=6(種)排列.例如:包含“1”“2”“3”這3個點的組合,就有(1,2,3)(1,3,2)(2,1,3)(2,3,1)(3,1,2)(3,2,1)共6種不同排列……像這樣,每個組合都重復了6次(即A33次),即組合數=排列數的1A33,故“在5個點中選取其中3個”對應組合數C35=A35A33=5×4×33×2×1=10(種).
填空:(1)A25=2020;
(2)A3m=m(m-1)(m-2)m(m-1)(m-2)(n≥3);
(3)C2n=n(n-1)2n(n-1)2(n≥2).
【問題提出2】在五邊形中,每次取其中的3個頂點連接成三角形,可以構造多少個三角形?
【問題解決2】
解:問題可以抽象成在5個點中取其中3個,有多少種組合.
∵C35=A35A33=5×4×33×2×1=10(種),
∴在5個點中取其中3個,有10種組合.
即在五邊形中,每次取其中的3個頂點連接成三角形,可以構造10個三角形.
【問題延伸】在六邊形中,每次取其中的4個頂點連接成四邊形,可以構造多少個四邊形?
(請仿照【問題解決2】利用排列、組合的計算方法解決問題)
【建立模型】在n(n≥3)邊形中,每次取其中的m(m≤n)個頂點連接成m角形,可以構造 n(n-1)……(n-m+1)m(m-1)(m-2)……2×1n(n-1)……(n-m+1)m(m-1)(m-2)……2×1個m邊形.
【模型應用】在如圖②所示的正方形網格圖中,以格點為頂點的三角形共有 1818個.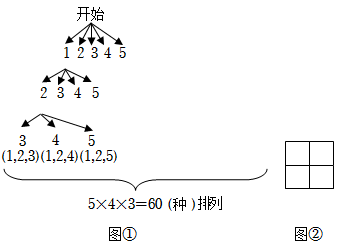
A
m
n
C
m
n
A
3
5
A
3
3
A
3
3
1
A
3
3
C
3
5
=
A
3
5
A
3
3
=
5
×
4
×
3
3
×
2
×
1
=
10
A
2
5
A
3
m
C
2
n
n
(
n
-
1
)
2
n
(
n
-
1
)
2
C
3
5
=
A
3
5
A
3
3
=
5
×
4
×
3
3
×
2
×
1
=
10
n
(
n
-
1
)
……
(
n
-
m
+
1
)
m
(
m
-
1
)
(
m
-
2
)
……
2
×
1
n
(
n
-
1
)
……
(
n
-
m
+
1
)
m
(
m
-
1
)
(
m
-
2
)
……
2
×
1
【考點】規律型:圖形的變化類;有理數的混合運算.
【答案】20;m(m-1)(m-2);;;18
n
(
n
-
1
)
2
n
(
n
-
1
)
……
(
n
-
m
+
1
)
m
(
m
-
1
)
(
m
-
2
)
……
2
×
1
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:258引用:2難度:0.4
相似題
-
1.將一列有理數-1,2,-3,4,-5,6,…,如圖所示有序排列.根據圖中的排列規律可知,有理數4在“峰1”中C的處.則有理數-2021在( )
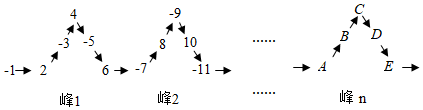
A.峰403E處 B.峰403D處 C.峰404D處 D.峰404E處 發布:2025/5/24 23:0:1組卷:274引用:3難度:0.6 -
2.如圖各圖形是由大小相同的黑點組成,圖1中有2個點,圖2中有7個點,圖3中有14個點,…,按此規律,第10個圖中黑點的個數是.
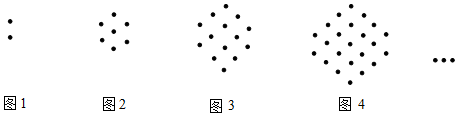 發布:2025/5/24 21:30:1組卷:823引用:10難度:0.6
發布:2025/5/24 21:30:1組卷:823引用:10難度:0.6 -
3.在邊長為1的正方形網格中,按下列方式得到“⊥”形圖形,第①個“⊥”形圖形的周長是10,則第n個“⊥”形圖形的周長是
. 發布:2025/5/24 22:30:1組卷:123引用:7難度:0.7
發布:2025/5/24 22:30:1組卷:123引用:7難度:0.7


