當前位置：試卷中心 > 試卷詳情

2022-2023學年山東省青島大學附中八年級（上）期末數(shù)學試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題（本大題共7小題，共21.0分．在每小題列出的選項中，選出符合題目的一項）

1．下列各數(shù)中1.141，
3
27
，π，
-
2
，0，4.217，0.1010010001，無理數(shù)有（　　）
A．2個 B．3個 C．4個 D．5個
組卷：143引用：2難度：0.8
解析

2．下列命題中是假命題的是（　　）

A．兩直線平行，同旁內(nèi)角互補

B．命題“（-4）²＞9，-4＜3”可以作為反例用來證明命題“若x²＞9，則x＞3”是假命題

C．若a∥b,a⊥c,那么b⊥c

D．相等的角是對頂角

組卷：313引用：2難度：0.7

解析

3．如圖是丁丁畫的一張臉的示意圖，如果用（-2，2）表示左眼，用（0，2）表示右眼，那么嘴的位置可以表示成（　　）
A．（1，0） B．（-1，0） C．（-1，1） D．（1，-1）
組卷：893引用：6難度：0.5
解析
4．若關(guān)于x,y的二元一次方程組
x
+
y
=
5
k
x
-
y
=
9
k
的解也是二元一次方程2x+3y=6的解，則k的值為（　　）
A．-
3
4
B．
3
4
C．
4
3
D．-
4
3
組卷：15991引用：90難度：0.9
解析
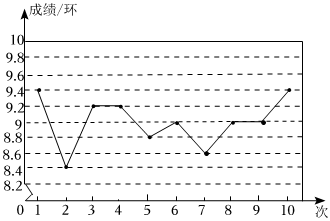5．某次射擊比賽，甲隊員的成績?nèi)鐖D，根據(jù)此統(tǒng)計圖，下列結(jié)論中錯誤的是（　　）
A．最高成績是9.4環(huán)
B．平均成績是9環(huán)
C．這組成績的眾數(shù)是9環(huán)
D．這組成績的方差是8.7環(huán)²
組卷：485引用：5難度：0.7
解析
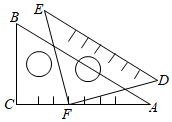6．如圖，將一副三角尺按圖中所示位置擺放，點F在AC上，其中∠ACB=90°，∠ABC=60°，∠EFD=90°，∠DEF=45°，AB∥DE，則∠AFD的度數(shù)是（　　）
A．15° B．30° C．45° D．60°
組卷：1874引用：48難度：0.8
解析
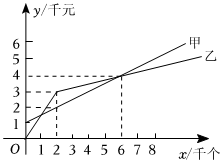7．某單位準備印制一批證書，現(xiàn)有兩個印刷廠可供選擇，甲廠費用分為制版費和印刷費兩部分，乙廠直接按印刷數(shù)量收取印刷費．甲、乙兩廠的印刷費用y（千元）與證書數(shù)量x（千個）的函數(shù)關(guān)系圖分別如圖中甲、乙所示，下列三種說法：
①甲廠的制版費為1千元；
②當印制證書超過2千個時，乙廠的印刷費用為0.2元/個；
③當印制證書8千個時，應選擇乙廠，可節(jié)省費用500元．
其中正確的說法有（　　）
A．①② B．②③ C．①③ D．①②③
組卷：1018引用：5難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

三、解答題（本大題共8小題，共78.0分）

21．【閱讀理解】
排列：從n個元素中選取m（m≤n）個元素，這m個元素稱為一個排列，不同順序視作不同排列，排列數(shù)量記作
A
m
n
．
組合：從n個元素中選取m（m≤n）個元素，這m個元素稱為一個組合，不同順序視作同一組合，組合數(shù)量記作
C
m
n
．
例如：（甲、乙），（乙、甲）是兩種不同的排列，確實同一種組合．
【問題提出1】在5個點中選取其中3個，有多少種排列？有多少種組合？
【問題解決1】
將5個點分別編號為“1”“2”“3”“4”“5”．
（一）排列：
（1）選取第1個點：
如圖①，從全部5個點中選取1個，有5種情況；
（2）選取第2個點：
如圖①，從剩余4個點中選取1個，有4種情況；
（3）選取第3個點：
如圖①，從剩余3個點中選取1個，有3種情況；
綜上所述，從5個點中任選3個點，共有5×4×3=60種排列，即
A
3
5
=60．
（二）組合：
因為每個組合都包含了3個點，所有每3個點共有
A
3
3
=3×2×1=6（種）排列．例如：包含“1”“2”“3”這3個點的組合，就有（1，2，3）（1，3，2）（2，1，3）（2，3，1）（3，1，2）（3，2，1）共6種不同排列……像這樣，每個組合都重復了6次（即
A
3
3
次），即組合數(shù)=排列數(shù)的
1
A
3
3
，故“在5個點中選取其中3個”對應組合數(shù)
C
3
5
=
A
3
5
A
3
3
=
5
×
4
×
3
3
×
2
×
1
=
10
（種）．
填空：（1）
A
2
5
=
；
（2）
A
3
m
=
（n≥3）；
（3）
C
2
n
=
（n≥2）．
【問題提出2】在五邊形中，每次取其中的3個頂點連接成三角形，可以構(gòu)造多少個三角形？
【問題解決2】
解：問題可以抽象成在5個點中取其中3個，有多少種組合．
∵
C
3
5
=
A
3
5
A
3
3
=
5
×
4
×
3
3
×
2
×
1
=
10
（種），
∴在5個點中取其中3個，有10種組合．
即在五邊形中，每次取其中的3個頂點連接成三角形，可以構(gòu)造10個三角形．
【問題延伸】在六邊形中，每次取其中的4個頂點連接成四邊形，可以構(gòu)造多少個四邊形？
（請仿照【問題解決2】利用排列、組合的計算方法解決問題）
【建立模型】在n（n≥3）邊形中，每次取其中的m（m≤n）個頂點連接成m角形，可以構(gòu)造
個m邊形．
【模型應用】在如圖②所示的正方形網(wǎng)格圖中，以格點為頂點的三角形共有
個．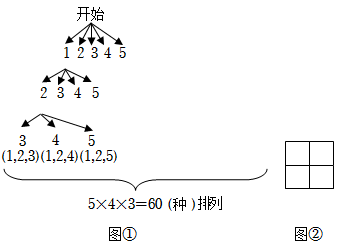
組卷：258引用：2難度：0.4
解析
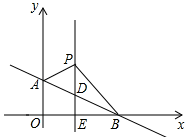22．如圖，平面直角坐標系中，直線AB：y=-
1
3
x+b交y軸于點A（0，1），交x軸于點B．過點E（1，0）且垂直于x軸的直線DE交AB于點D，P是直線DE上一動點，且在點D的上方，設P（1，n）．
（1）求直線AB的解析式和點B的坐標；
（2）求△ABP的面積（用含n的代數(shù)式表示）；
（3）當△ABP的面積為2時，以PB為邊在第一象限作等腰直角三角形BPC，求出點C的坐標．
組卷：1972引用：6難度：0.5
解析