“趙爽弦圖”巧妙地利用面積關(guān)系證明了勾股定理，是我國古代數(shù)學的驕傲，如圖所示的“趙爽弦圖”是由四個全等的直角三角形和一個小正方形拼成一個大正方形，設(shè)直角三角形較長直角邊長為a,較短直角邊長為b,若ab=24，大正方形的面積為129，則小正方形的邊長為（ ）
【考點】勾股定理的證明．
【答案】A
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/30 8:0:9組卷：595引用：7難度：0.5
相似題
-
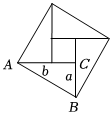1．如圖，“趙爽弦圖”由4個全等的直角三角形所圍成，在Rt△ABC中，AC=b,BC=a,∠ACB=90°，若圖中大正方形的面積為35，小正方形的面積為3，則（a+b）2的值為 ．發(fā)布：2025/5/24 13:0:1組卷：69引用：1難度：0.6 -
2．小慧在課外閱讀時遇到了一個與勾股定理有關(guān)的故事：古希臘哲學家柏拉圖對勾股定理很有研究，曾得到勾股數(shù)的一個結(jié)論：如果m表示大于1的整數(shù)，則a=2m,b=m2-1，c=m2+1構(gòu)成勾股數(shù)，你能證明柏拉圖這個結(jié)論嗎？并利用這個結(jié)論寫出兩組勾股數(shù)．（勾股數(shù)定義：若三角形三邊長a、b、c都是正整數(shù)，且滿足a2+b2=c2，那么a、b、c稱為一組勾股數(shù)）．
發(fā)布：2025/5/25 1:0:1組卷：28引用：1難度：0.5 -
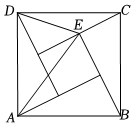3．漢代數(shù)學家趙爽為了證明勾股定理，構(gòu)造了一副“弦圖”，后人稱其為“趙爽弦圖”．如圖，大正方形ABCD由四個全等的直角三角形和一個小正方形組成，若∠ADE=∠AED，，則△ADE的面積為（ ）AD=25發(fā)布：2025/5/25 11:30:2組卷：357引用：3難度：0.5