某研究性學(xué)習(xí)小組在學(xué)習(xí)《簡單的圖案設(shè)計》時,發(fā)現(xiàn)了一種特殊的四邊形,如圖1,在四邊形ABCD中,AB=AD,∠B+∠D=180°,我們把這種四邊形稱為“等補四邊形”.
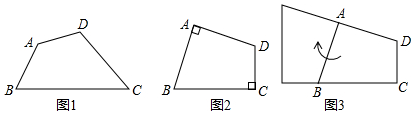
如何求“等補四邊形”的面積呢?
探究一:
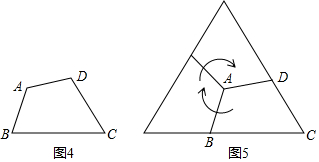
如圖2,已知“等補四邊形”ABCD,若∠A=90°,將“等補四邊形”ABCD燒點A順時針旋轉(zhuǎn)90°,可以形成一個直角梯形(如圖3).若BC=4cm,CD=2cm,則“等補四邊形”ABCD的面積為 99cm2.
探究二:
如圖4,已知“等補四邊形”ABCD,若∠A=120,將“等補四邊形”ABCD繞點A順時針旋轉(zhuǎn)120°,再將得到的四邊形按上述方式旋轉(zhuǎn)120°,可以形成一個等邊三角形(如圖5).若BC=6cm,CD=4cm,則“等補四邊形”ABCD的面積為 25332533cm2.
由以上探究可知,對一些特殊的“等補四邊形”,只需要知道BC,CD的長度,就可以求它的面積.那么,如何求一般的“等補四邊形”的面積呢?
探究三:
如圖6,已知“等補四邊形”ABCD,連接AC,將△ACD以點A為旋轉(zhuǎn)中心順時針旋轉(zhuǎn)一定角度,使AD與AB重合,得到△ABC′,點C的對應(yīng)點為點C′.
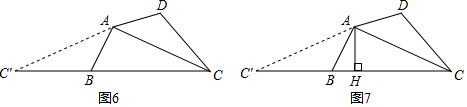
Ⅰ.由旋轉(zhuǎn)得:∠D=∠ABC′ABC′,因為∠ABC+∠D=180°,所以∠ABC+∠ABC'=180°,即點C',B,C在同一直線上,所以我們拼成的圖形是一個三角形,即△ACC'.
Ⅱ.如圖7,在△ACC'中,作AH⊥BC于點H,若AH=m,CH=n,試求出“等補四邊形”ABCD的面積(用含m,n的代數(shù)式表示),并說明理由.
探究四:
以下是圖7中的“等補四邊形”ABCD的四個條件:①BC=14cm;②CD=10cm;③AH=5cm;④AC=13cm.請你從中選擇不超過3個條件(不能有多余條件),并用所選擇的條件計算圖7中的“等補四邊形”ABCD的面積.
選擇的條件是:①②③①②③; ③④③④(寫出兩種不同組合,只填寫序號).“等補四邊形”ABCD的面積為 6060cm2.
25
3
3
25
3
3
【考點】四邊形綜合題.
【答案】9;;ABC′;①②③;③④;60
25
3
3
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:1692引用:3難度:0.1
相似題
-
1.如圖,四邊形ABCD、EBGF都是正方形.
(1)如圖1,若AB=4,EC=,求FC的長;17
(2)如圖2,正方形EBGF繞點B逆時針旋轉(zhuǎn),使點G正好落在EC上,猜想AE、EB、EC之間的數(shù)量關(guān)系,并證明你的結(jié)論;
(3)如圖3,在(2)條件下,∠BCE=22.5°,EC=2,點M為直線BC上一動點,連接EM,過點M作MN⊥EC,垂足為點N,直接寫出EM+MN的最小值.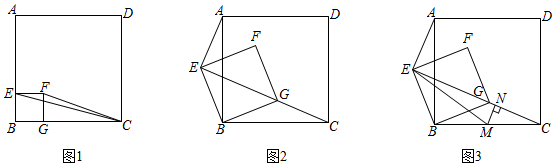 發(fā)布:2025/5/24 19:0:1組卷:233引用:2難度:0.5
發(fā)布:2025/5/24 19:0:1組卷:233引用:2難度:0.5 -
2.如圖1,在菱形ABCD中,AB=10,∠BAD=α(0°<α<180°),連接AC,點Q是AD上的一點,連接BQ交AC于點E,過點E作EG⊥AD于點G,連接DE.
(1)當α=60°且時,DQAQ=12=,DG=;DEEQ
(2)當時,若S菱形ABCD=50時.求DG的長度;DQAQ=1
(3)當時,如圖2,分別以點E,A為圓心,大于DQAQ=1為半徑畫弧.交于點F和H,作直線FH,分別交AB,AC,AD于點P,N,M,請你判斷點M的位置是否變化?若不變,求AM的長;若變化說明理由.12AE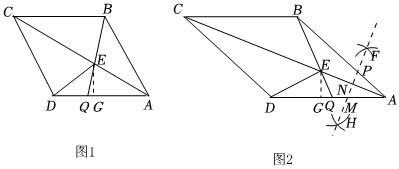 發(fā)布:2025/5/24 19:0:1組卷:88引用:4難度:0.3
發(fā)布:2025/5/24 19:0:1組卷:88引用:4難度:0.3 -
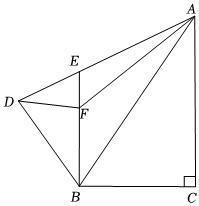 3.如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=,把Rt△ABC沿AB翻折得到Rt△ABD,過點B作BE⊥BC,交AD于點E,點F是線段BE上一點,且tan∠ADF=3.則下列結(jié)論中:①AE=BE;②△BED∽△ABC;③BD2=AD?DE;④AF=32.正確的有 .(把所有正確答案的序號都填上)2133發(fā)布:2025/5/24 19:30:1組卷:526引用:3難度:0.3
3.如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=,把Rt△ABC沿AB翻折得到Rt△ABD,過點B作BE⊥BC,交AD于點E,點F是線段BE上一點,且tan∠ADF=3.則下列結(jié)論中:①AE=BE;②△BED∽△ABC;③BD2=AD?DE;④AF=32.正確的有 .(把所有正確答案的序號都填上)2133發(fā)布:2025/5/24 19:30:1組卷:526引用:3難度:0.3


