2022-2023學年廣東省深圳市華附集團校九年級（上）期末數學試卷

一、選擇題（共10小題，共30分）

• 1．唐代李白《日出行》云：“日出東方隈，似從地底來”．描述的是看日出的景象，意思是太陽從東方升起，似從地底而來．如圖所示，此時觀測到地平線和太陽所成的視圖可能是（　　）

  A．

  B．

  C．

  D．
  組卷：687引用：6難度：0.7

  解析

• 2．下列方程是一元二次方程的是（　　）

  A．x+1=0

  B．2x＞2

  C． 1 x = 4

  D．x2+1=5
  組卷：439引用：4難度：0.8

  解析

• 3．如圖，直線l₁∥l₂∥l₃，分別交直線m、n于點A、B、C、D、E、F．若AB：BC=5：3，DE=15，則EF的長為（　　）

  A．6

  B．9

  C．10

  D．25
  組卷：3246引用：17難度：0.7

  解析

• 4．若點A（-2，1）在反比例函數y=

  k

  x

  的圖象上，則k的值是（　　）

  A．2

  B．-2

  C． 1 2

  D．- 1 2
  組卷：725引用：3難度：0.6

  解析

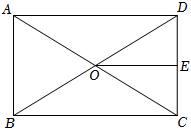• 5．如圖，矩形ABCD的對角線AC、BD相交于點O，點E是CD的中點，若OE=3，則BC的長為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：2148引用：14難度：0.8

  解析

• 6．如圖，以點O為位似中心，把△ABC放大為原圖形的2倍得到△A'B'C'，以下說法中錯誤的是（　　）

  A．△ABC∽△A'B'C'

  B．點C、點O、點C'三點在同一直線上

  C．AO：AA'=1：2

  D．AB∥A'B'
  組卷：1755引用：12難度：0.5

  解析

• 7．某校舉行演講比賽，小李、小吳與另外兩位同學闖入決賽，則小李和小吳獲得前兩名的概率是（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 1 6
  組卷：1153引用：8難度：0.5

  解析

三、解答題（共7小題，共55分）

• 21．以下各圖均是由邊長為1的小正方形組成的網格，圖中的點A、B、C、D均在格點上．
  （1）在圖①中，PC：PB=

  ．
  （2）利用網格和無刻度的直尺作圖，保留痕跡，不寫作法．
  ①如圖②，在AB上找一點P，使AP=3．
  ②如圖③，在BD上找一點P，使△APB∽△CPD．
  
  組卷：3167引用：44難度：0.7

  解析

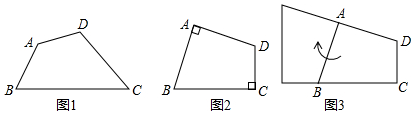
• 22．某研究性學習小組在學習《簡單的圖案設計》時，發現了一種特殊的四邊形，如圖1，在四邊形ABCD中，AB=AD，∠B+∠D=180°，我們把這種四邊形稱為“等補四邊形”．
  
  如何求“等補四邊形”的面積呢？
  探究一：
  如圖2，已知“等補四邊形”ABCD，若∠A=90°，將“等補四邊形”ABCD燒點A順時針旋轉90°，可以形成一個直角梯形（如圖3）．若BC=4cm,CD=2cm,則“等補四邊形”ABCD的面積為

  cm²．
  探究二：
  如圖4，已知“等補四邊形”ABCD，若∠A=120，將“等補四邊形”ABCD繞點A順時針旋轉120°，再將得到的四邊形按上述方式旋轉120°，可以形成一個等邊三角形（如圖5）．若BC=6cm,CD=4cm,則“等補四邊形”ABCD的面積為

  cm²．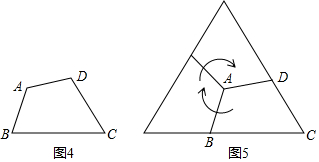
  
  由以上探究可知，對一些特殊的“等補四邊形”，只需要知道BC，CD的長度，就可以求它的面積．那么，如何求一般的“等補四邊形”的面積呢？
  探究三：
  如圖6，已知“等補四邊形”ABCD，連接AC，將△ACD以點A為旋轉中心順時針旋轉一定角度，使AD與AB重合，得到△ABC′，點C的對應點為點C′．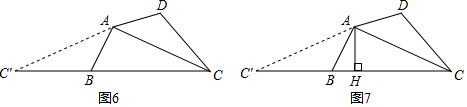
  
  Ⅰ．由旋轉得：∠D=∠

  ，因為∠ABC+∠D=180°，所以∠ABC+∠ABC'=180°，即點C'，B，C在同一直線上，所以我們拼成的圖形是一個三角形，即△ACC'．
  Ⅱ．如圖7，在△ACC'中，作AH⊥BC于點H，若AH=m,CH=n,試求出“等補四邊形”ABCD的面積（用含m,n的代數式表示），并說明理由．
  探究四：
  以下是圖7中的“等補四邊形”ABCD的四個條件：①BC=14cm；②CD=10cm；③AH=5cm；④AC=13cm.請你從中選擇不超過3個條件（不能有多余條件），并用所選擇的條件計算圖7中的“等補四邊形”ABCD的面積．
  選擇的條件是：

  ；

  （寫出兩種不同組合，只填寫序號）．“等補四邊形”ABCD的面積為

  cm²．
  組卷：1692引用：3難度：0.1

  解析