某種新型電子產(chǎn)品,每件制造成本為18元,試銷過程中發(fā)現(xiàn),每月銷售量y(萬件)與銷售單價x(元)之間的關(guān)系可以近似地看作一次函數(shù)y=-2x+100.
(1)寫出每月的利潤W(萬元)與銷售單價x(元)之間的函數(shù)關(guān)系式;
(2)物價部門規(guī)定該產(chǎn)品銷售單價不低于成本且不高于33元.當(dāng)銷售單價為多少元時,廠商每月能獲得最大利潤?最大利潤是多少?
【考點】二次函數(shù)的應(yīng)用.
【答案】(1)每月的利潤W(萬元)與銷售單價x(元)之間的函數(shù)關(guān)系式為W=-2x2+136x-1800;
(2)當(dāng)銷售單價為33元時,廠商每月能獲得最大利潤,最大利潤是510元.
(2)當(dāng)銷售單價為33元時,廠商每月能獲得最大利潤,最大利潤是510元.
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:12引用:1難度:0.5
相似題
-
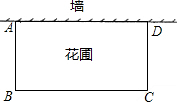 1.張大爺要圍成一個矩形花圃.花圃的一邊利用足夠長的墻另三邊用總長為32米的籬笆恰好圍成.圍成的花圃是如圖所示的矩形ABCD.設(shè)AB邊的長為x米.矩形ABCD的面積為S平方米.
1.張大爺要圍成一個矩形花圃.花圃的一邊利用足夠長的墻另三邊用總長為32米的籬笆恰好圍成.圍成的花圃是如圖所示的矩形ABCD.設(shè)AB邊的長為x米.矩形ABCD的面積為S平方米.
(1)求S與x之間的函數(shù)關(guān)系式(不要求寫出自變量x的取值范圍);
(2)當(dāng)x為何值時,S有最大值并求出最大值.
(參考公式:二次函數(shù)y=ax2+bx+c(a≠0),當(dāng)x=-時,y最大(小)值=b2a)4ac-b24a發(fā)布:2025/6/24 19:0:1組卷:251引用:25難度:0.5 -
2.俄羅斯世界杯足球賽期間,某商店銷售一批足球紀(jì)念冊,每本進(jìn)價40元,規(guī)定銷售單價不低于44元,且獲利不高于30%.試銷售期間發(fā)現(xiàn),當(dāng)銷售單價定為44元時,每天可售出300本,銷售單價每上漲1元,每天銷售量減少10本,現(xiàn)商店決定提價銷售.設(shè)每天銷售量為y本,銷售單價為x元.
(1)請直接寫出y與x之間的函數(shù)關(guān)系式和自變量x的取值范圍;
(2)當(dāng)每本足球紀(jì)念冊銷售單價是多少元時,商店每天獲利2400元?
(3)將足球紀(jì)念冊銷售單價定為多少元時,商店每天銷售紀(jì)念冊獲得的利潤w元最大?最大利潤是多少元?發(fā)布:2025/6/25 6:30:1組卷:6496引用:40難度:0.3 -
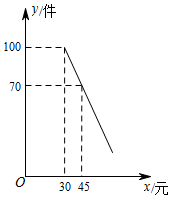 3.為迎接國慶節(jié),某商店購進(jìn)了一批成本為每件30元的紀(jì)念商品,經(jīng)調(diào)查發(fā)現(xiàn),該商品每天的銷售量y(件)與銷售單價x(元)滿足一次函數(shù)關(guān)系,其圖象如圖所示.
3.為迎接國慶節(jié),某商店購進(jìn)了一批成本為每件30元的紀(jì)念商品,經(jīng)調(diào)查發(fā)現(xiàn),該商品每天的銷售量y(件)與銷售單價x(元)滿足一次函數(shù)關(guān)系,其圖象如圖所示.
(1)求該商品每天的銷售量y與銷售單價x的函數(shù)關(guān)系式;
(2)若商店按不低于成本價,且不高于60元的單價銷售,則銷售單價定為多少元,才能使銷售該商品每天獲得的利潤w(元)最大?最大利潤是多少?發(fā)布:2025/6/25 8:30:1組卷:926引用:7難度:0.7


