2019-2020學年云南省大理州祥云縣九年級（上）期末數學試卷

一、填空題（本大題共6小題，每小題3分，共18分）

• 1．一元二次方程3x²=x的根是

   

  ．
  組卷：459引用：14難度：0.5

  解析

• 2．二次函數y=-2（x-2）²+1的對稱軸為

  ．
  組卷：12引用：1難度：0.7

  解析

• 3．如圖，四邊形ABCD是⊙O的內接四邊形，若∠BOD=130°，則∠A=

  ．
  組卷：13引用：1難度：0.7

  解析

• 4．圓錐的側面展開圖的圓心角是120°，其底面圓的半徑為2cm,則其側面展開圖的半徑為

  cm.
  組卷：11引用：1難度：0.7

  解析

• 5．將拋物線y=（x+2）²-1先向上平移2個單位，再向左平移1個單位后，得到的拋物線解析式為

  ．
  組卷：17引用：1難度：0.7

  解析

• 6．給出下列函數①y=3x+1；②y=-2x；③

  y

  =

  -

  1

  5

  x

  2

  ．從中任取一個函數，則取出的函數符合條件“當x＞1時，函數值y隨x的增大而減小”的概率是

  ．
  組卷：3引用：1難度：0.6

  解析

二、選擇題（本大題共8小題，每小題只有一個正確選項，每小題4分，共32分）

• 7．如所示圖形既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：3引用：1難度：0.8

  解析

三、解答題（本大題共9小題，共70分）

• 22．某種新型電子產品，每件制造成本為18元，試銷過程中發現，每月銷售量y（萬件）與銷售單價x（元）之間的關系可以近似地看作一次函數y=-2x+100．
  （1）寫出每月的利潤W（萬元）與銷售單價x（元）之間的函數關系式；
  （2）物價部門規定該產品銷售單價不低于成本且不高于33元．當銷售單價為多少元時，廠商每月能獲得最大利潤？最大利潤是多少？
  組卷：12引用：1難度：0.5

  解析

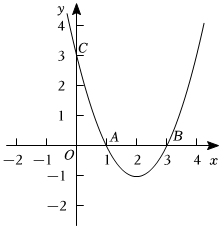• 23．如圖，已知拋物線y=ax²+bx+c與x軸相交于A、B兩點，與y軸相交于點C（0，3），且OA=1，OB=3．
  （1）求拋物線的函數關系式；
  （2）若點D（4，3）是拋物線y=ax²+bx+c上的一點，那么在拋物線的對稱軸上，是否存在一點P，使得△BDP的周長最小？若存在，請求出點P的坐標；若不存在，請說明理由．
  組卷：21引用：1難度：0.5

  解析