如圖，直線AB：y=kx+b（k≠0）過點A（2，2），B（1，4）．
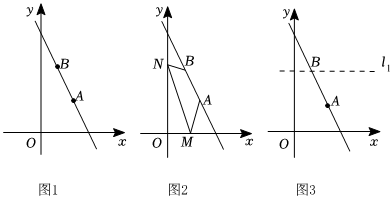
（1）求直線AB的解析式；
（2）如圖2，點M，點N分別為x軸，y軸上一動點，求AM+MN+NB的最小值及此時點M的坐標；
（3）如圖3，在（2）問的條件下，過點B作l1垂直于y軸，點P為直線AB上一動點，點Q為直線l1上一動點，若△MPQ是以MQ為腰的等腰直角三角形，直接寫出所有滿足條件的點Q坐標．
【考點】一次函數綜合題．
【答案】（1）直線AB解析式為y=-2x+6；
（2）（1，0）；
（3）點Q坐標為（13，4）或（5，4）或（-7，4）或（，4）．
（2）（1，0）；
（3）點Q坐標為（13，4）或（5，4）或（-7，4）或（
11
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/11 8:0:9組卷：1728引用：1難度：0.1
相似題
-
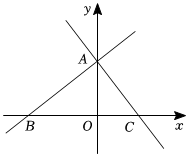1．如圖，在平面直角坐標系中，直線y=kx+b與x軸交于點B（-5，0），與y軸交于點A，直線過點A，與x軸交于點C，點P是x軸上方一個動點．y=-43x+4
（1）求直線AB的函數表達式；
（2）若點P在線段AB上，且S△APC=S△AOB，求點P的坐標；
（3）當 S△PBC=S△ABC時，動點M從點B出發，先運動到點P，再從點P運動到點C后停止運動．點M的運動速度始終為每秒1個單位長度，運動的總時間為t（秒），請直接寫出t的最小值．發布：2025/5/22 18:30:2組卷：670引用：1難度：0.3 -
2．給出如下定義：對于線段PQ，以點P為中心，把點Q逆時針旋轉60°得到點R，點R叫做線段PQ關于點P的“完美點”．
例如等邊△ABC中，點C就是線段AB關于點A的“完美點”．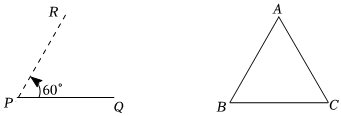
在平面直角坐標系xOy中．
（1）已知點A（0，2），在A1（，1），A2（-3，1），A3（1，3），A4（1，-3）中，是線段OA關于點O的“完美點”；3
（2）直線y=x+4上存在線段BB′，若點B′恰好是線段BO關于點B的“完美點”，求線段BB′的長；
（3）若OC=4，OE=2，點D是線段OC關于點O的“完美點”，點F是線段EO關于點E的“完美點”．當線段DF分別取得最大值和最小值時，直接寫出線段CE的長．發布：2025/5/22 15:30:1組卷：595引用：1難度：0.1 -
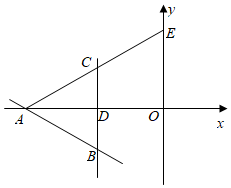3．如圖，直線y=-x-6與x軸交于點A，點B（-6，m）也在該直線上，點B關于x軸的對稱點為點C，直線BC交x軸于點D，點E坐標為（0，12）．112
（1）m的值為 ，點C的坐標為 ；
（2）求直線AC的函數表達式；
（3）晶晶有個想法：“設S=S△ABD+S四邊形DCEO.由點B與點C關于x軸對稱易得S△ABD=S△ACD，而△ACD與四邊形DCEO拼接后可看成△AOE，這樣求S便轉化為直接求△AOE的面積．”但經反復演算，發現S△AOE≠S，請通過計算解釋她的想法錯在哪里？發布：2025/5/23 2:30:1組卷：268引用：4難度：0.5