從2開始，連續的偶數相加，它們和的情況如表：
| 加數的個數n | S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
56
56
．（2）根據表中的規律猜想：用含n的代數式表示S的公式為：S=2+4+6+8+…+2n=
n（n+1）
n（n+1）
．（3）根據上題的規律計算102+104+106+…+2020的值（要有過程）．
【考點】規律型：數字的變化類．
【答案】56；n（n+1）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/12 20:0:8組卷：102引用：3難度：0.6
相似題
-
1．數1，2，3，…，k2按下列方式排列：
任取其中一數，并劃去該數所在的行與列；這樣做了k次后，所取出的k個數的和是1 2 … k k+1 k+2 … 2k … （k-1）k+1 （k-1）k+2 … k2 ．發布：2025/5/28 0:0:1組卷：36引用：1難度：0.7 -
2．觀察下列各式：
152=1×（1+1）×100+52=225，
252=2×（2+1）×100+52=625，
352=3×（3+1）×100+52=1225，
…
依此規律，第n個等式（n為正整數）為．發布：2025/5/28 0:0:1組卷：217引用：8難度：0.5 -
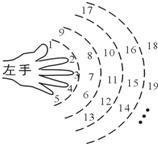3．如圖，在小時候，我們就用手指練習過數數．一個小朋友按如圖所示的規則練習數數，數到2009時對應的指頭是（填出指頭的名稱，各指頭的名稱依次為大拇指、食指、中指、無名指、小指）．發布：2025/5/28 0:0:1組卷：141引用：30難度：0.7