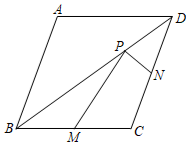
如圖，菱形ABCD的兩條對角線的長分別為6和8，M、N分別是邊BC、CD的中點，P是對角線BD上一點，則PM+PN的最小值為（ ）
【考點】軸對稱-最短路線問題；菱形的性質(zhì)．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：337引用：4難度：0.5
相似題
-
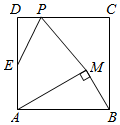1．如圖，動點M在邊長為2的正方形ABCD內(nèi)，且AM⊥BM，P是CD邊上的一個動點，E是AD邊的中點，則線段PE+PM的最小值為（ ）發(fā)布：2025/5/21 15:0:1組卷：2997引用：9難度：0.4 -
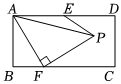2．如圖，在矩形ABCD中，E是AD的中點，點F在BC邊上，點P在矩形ABCD內(nèi)部，AF=PF，AF⊥PF，連接AP，EP．若AB=1，BC=2，則AP+EP的最小值等于（ ）發(fā)布：2025/5/21 16:0:1組卷：202引用：3難度：0.4 -
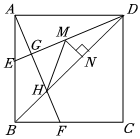3．如圖，正方形ABCD的邊長為4，DE平分∠ADB交AB于點E，在BC上截取BF=AE，連接AF，交DE于點G，交BD于點H，點M是線段DG上一個動點，MN⊥BD于點N．下列說法：①△ADE≌△BAF；②DE⊥AF；③；④MN+MH的最小值是DH=23．正確的是 （只填序號）．22發(fā)布：2025/5/21 16:0:1組卷：247引用：3難度：0.7