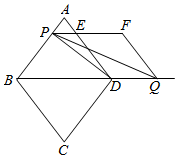
如圖，在菱形ABCD中，AB=10cm,對角線BD=12cm.動點P從點A出發(fā)，以1cm/s的速度沿AB勻速運動；動點Q同時從點D出發(fā)，以2cm/s的速度沿BD的延長線方向勻速運動．當(dāng)點P到達點B時，點P，Q同時停止運動．設(shè)運動時間為t（s）（0＜t≤10），過點P作PE∥BD，交AD于點E，以DQ，DE為邊作?DQFE，連接PD，PQ．
（1）當(dāng)t為何值時，△BPQ為直角三角形？
（2）設(shè)四邊形BPFQ的面積為S（cm2），求S與t的函數(shù)關(guān)系式；
（3）在運動過程中，是否存在某一時刻t,使四邊形BPFQ的面積為菱形ABCD面積的1924？若存在，求出t的值；若不存在，請說明理由；
（4）是否存在某一時刻t,使點F在∠ABD的平分線上？若存在，求出t的值；若不存在，請說明理由．
19
24
【考點】四邊形綜合題．
【答案】（1）當(dāng)t為時，△BPQ為直角三角形．
（2）S=．
（3）當(dāng)t的值5為或時，四邊形BPFQ的面積為菱形ABCD面積的．
（4）t=時，點F在∠ABD的平分線上．
14
11
（2）S=
-
52
25
t
2
+
16
t
+
48
（3）當(dāng)t的值5為或
35
13
19
24
（4）t=
50
21
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/25 19:0:2組卷：466引用：2難度：0.1
相似題
-
1．【問題情境】
如圖1，在等腰直角三角形ABC中，∠ACB=90°，F(xiàn)是AC邊上一動點（點F不與點A，C重合），以CF為邊在△ABC外作正方形CDEF，連接AD，BF．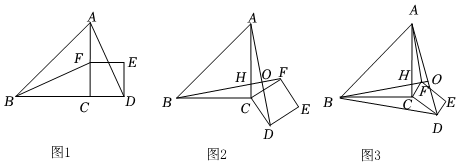
【探究展示】
（1）①猜想：圖1中，線段BF，AD的數(shù)量關(guān)系是 ，位置關(guān)系是 ．
②如圖2，將圖1中的正方形CDEF繞點C順時針旋轉(zhuǎn)α，BF交AC于點H，交AD于點O，①中的結(jié)論是否仍然成立？請說明理由．
【拓展延伸】
（2）如圖3，將【問題情境】中的等腰直角三角形ABC改為直角三角形ABC，∠ACB=90°，正方形CDEF改為矩形CDEF，連接BF并延長，交AC于點H，交AD于點O，連接BD，AF．若AC=4，BC=3，CD=，CF=1，求BD2+AF2的值．43發(fā)布：2025/5/25 23:30:1組卷：246引用：3難度：0.4 -
2．已知△CAB和△CDE均為等腰直角三角形，∠DCE=∠ACB=90°．
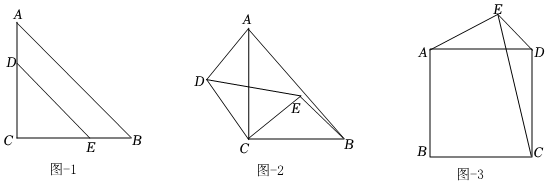
發(fā)現(xiàn)：如圖-1，點D落在AC上，點E落在CB上，則直線AD和直線BE的位置關(guān)系是 ；線段AD和線段BE的數(shù)量關(guān)系是 ．
探究：在圖-1的基礎(chǔ)上，將△CDE繞點C逆時針旋轉(zhuǎn)，得到圖-2．
求證：（1）AD=BE，（2）BE⊥AD．
應(yīng)用：如圖-3，四邊形ABCD是正方形，E是平面上一點，且AE=3，DE=．2
直接寫出CE的取值范圍．發(fā)布：2025/5/26 0:0:1組卷：84引用：2難度：0.4 -
3．已知正方形ABCD，AB=4，點E是BC邊上一點（不與B、C重合），將EA繞點E順時針旋轉(zhuǎn)90°至EF，連接AF，設(shè)EF交CD于點P，AF交CD于點Q．
（1）如圖1，線段EQ、BE與DQ之間有怎樣的數(shù)量關(guān)系，請證明你的發(fā)現(xiàn)；
（2）如圖2，連接DF，則AF+DF的最小值是 （直接寫出答案）；
（3）如圖3，連接CF，①若BE=m,用m的代數(shù)式表示；FPPE
②若m=4-4，求∠EQF的度數(shù)．2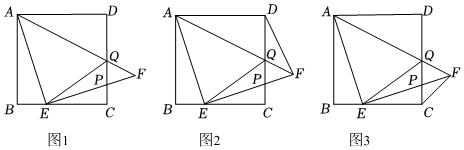
發(fā)布：2025/5/26 0:0:1組卷：252引用：1難度：0.3
相關(guān)試卷