試卷征集
          
                
          
            
          
            
          
                
          
                    
                    
          加入會員
          
                
          
            
          
            
          
                
          
                    
                    
          操作視頻
          
                
          
            
          
        
          
    
          

    
          
        
    
          
    
          
    
          
        
          
            



          
    
          
        
          
            
          設F1，F2是橢圓C1：
          x
          2
          a
          1
          2
          +
          y
          2
          b
          1
          2
          =1（a1＞b1＞0）與雙曲線C2：
          x
          2
          a
          2
          2
          -
          y
          2
          b
          2
          2
          =1（a2＞0，b2＞0）的公共焦點，曲線C1，C2在第一象限內交于點M，∠F1MF2=60°，若橢圓的離心率
          e
          1
          ∈
          [
          3
          3
          ，
          1
          ）
          ，則雙曲線的離心率e2的取值范圍是（　　）
          【答案】B
          【解答】
          【點評】
          聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
          發布：2024/10/23 0:0:2組卷：345引用：8難度：0.5
          
        
          
            
          
                
          相似題
          
                
            
                        
          • 
                            
            1．橢圓
            x
            2
            25
            +
            y
            2
            b
            2
            =
            1
            （b＞0）與雙曲線
            x
            2
            8
            -
            y
            2
            =
            1
            有公共的焦點，則b=
            ．
            發布：2024/12/30 13:0:5組卷：187引用：7難度：0.8
            
                        
            • 
                        
          • 
                            
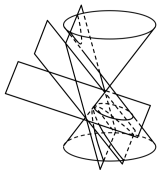            2．兩千多年前，古希臘大數學家阿波羅尼奧斯發現，用一個不垂直于圓錐的軸的平面截圓錐，其截口曲線是圓錐曲線（如圖）．已知圓錐軸截面的頂角為2θ，一個不過圓錐頂點的平面與圓錐的軸的夾角為α．當
            θ
            ＜
            α
            ＜
            π
            2
            時，截口曲線為橢圓；當α=θ時，截口曲線為拋物線；當0＜α＜θ時，截口曲線為雙曲線．在長方體ABCD-A1B1C1D1中，AB=AD=1，AA1=2，點P在平面ABCD內，下列說法正確的是（　　）
            發布：2024/12/11 15:30:1組卷：550引用：3難度：0.3
            
                        
            • 
                        
          • 
                            
            3．已知等軸雙曲線N的頂點分別是橢圓
            C
            ：
            x
            2
            6
            +
            y
            2
            2
            =
            1
            的左、右焦點F1、F2．
            （Ⅰ）求等軸雙曲線N的方程；
            （Ⅱ）Q為該雙曲線N上異于頂點的任意一點，直線QF1和QF2與橢圓C的交點分別為E，F和G，H，求|EF|+4|GH|的最小值．
            發布：2024/12/29 3:0:1組卷：352引用：3難度：0.6
            
                        
            • 
                
          
            
          
    
          
        

          

        
          
    
          
    
           
        
          APP開發者：深圳市菁優智慧教育股份有限公司| 應用名稱：菁優網 | 應用版本：5.0.7 |隱私協議|第三方SDK|用戶服務條款
          本網部分資源來源于會員上傳，除本網組織的資源外，版權歸原作者所有，如有侵犯版權，請立刻和本網聯系并提供證據，本網將在三個工作日內改正