（1）閱讀理解
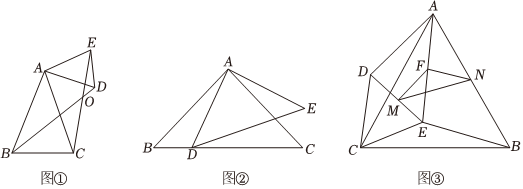
由兩個頂角相等且有公共頂角頂點的特殊多邊形組成的圖形，如果把它們的底角頂點連接起來，則在相對位置變化的過程中，始終存在一對全等三角形，我們把這種模型稱為“手拉手模型”．在如圖①所示的“手拉手”圖形中，小白發現若∠BAC=∠DAE，AB=AC，AD=AE，則△ABD≌△ACE，請證明他的發現；
（2）問題解決
如圖②，∠BAC=∠DAE=90°，AB=AC，AD=AE，試探索線段CD，BD，DE之間滿足的等量關系，并證明；
（3）拓展探究
如圖③，△ABC和△DEC是擁有公共頂點C的兩個等邊三角形，M點、N點、F點分別是DE、AB、AE的中點．當AD=10時，請直接寫出MN的長．
【考點】四邊形綜合題．
【答案】（1）見解析；
（2）BD2+CD2=DE2．理由見解析過程；
（3）．
（2）BD2+CD2=DE2．理由見解析過程；
（3）
MN
=
5
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/1 8:0:9組卷：362引用：2難度：0.5
相似題
-
1．連接四邊形不相鄰兩個頂點的線段叫做四邊形的對角線，如圖1，四邊形ABCD中線段AC、線段BD就是四邊形ABCD的對角線．把對角線互相垂直的四邊形叫做垂美四邊形．
（1）概念理解：如圖2，在四邊形ABCD中，AB=AD，CB=CD，問四邊形ABCD是垂美四邊形嗎？請說明理由．
（2）性質探究：試探索垂美四邊形ABCD兩組對邊AB，CD的平方和與BC，AD的平方和之間的數量關系．
猜想結論：（要求用文字語言敘述） ．
寫出證明過程（先畫出圖形，寫出已知、求證）．
（3）問題解決：如圖3，分別以Rt△ACB的直角邊AC和斜邊AB為邊向外作正方形ACFG和正方形ABDE，連接CE，BG，GE，已知AC=4，AB=5，求GE長．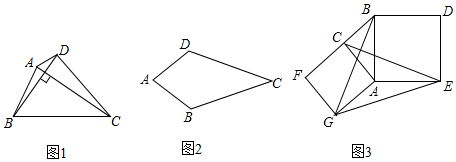
發布：2025/6/17 6:30:2組卷：304引用：2難度：0.5 -
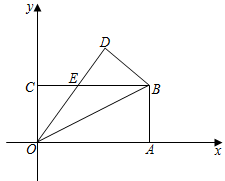2．如圖，在平面直角坐標系中，長方形OABC的頂點A、C分別在x軸、y軸的正半軸上．點B的坐標為（8，4），將該長方形沿OB翻折，點A的對應點為點D，OD與BC交于點E．
（Ⅰ）證明：EO=EB；
（Ⅱ）點P是直線OB上的任意一點，且△OPC是等腰三角形，求滿足條件的點P的坐標；
（Ⅲ）點M是OB上任意一點，點N是OA上任意一點，若存在這樣的點M、N，使得AM+MN最小，請直接寫出這個最小值．發布：2025/6/17 9:0:1組卷：305引用：2難度：0.3 -
3．感知：如圖①，在正方形ABCD中，點E在對角線AC上（不與點A、C重合），連接ED，EB，過點E作EF⊥ED，交邊BC于點F．易知∠EFC+∠EDC=180°，進而證出EB=EF．
探究：如圖②，點E在射線CA上（不與點A、C重合），連接ED、EB，過點E作EF⊥ED，交CB的延長線于點F．求證：EB=EF
應用：如圖②，若DE=2，CD=1，則四邊形EFCD的面積為．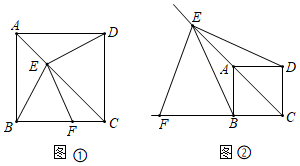
發布：2025/6/17 8:0:1組卷：250引用：5難度：0.3