2022-2023學年貴州省銅仁市八年級（下）期末數學試卷
發布：2024/8/1 8:0:9
一、選擇題：共12道題，每小題3分，共36分.
-
1．國家級非物質文化遺產松桃苗繡，構圖夸張浪漫，顏色素凈淡雅，以花鳥蟲魚，飛禽走獸等為題材，體現苗族人民向往自由與和平的精神世界，如所示四幅苗繡圖樣中，是中心對稱圖形的是（ ）
組卷：21引用：1難度：0.9 -
2．下列各數化簡后為負數的是（ ）
組卷：80引用：2難度：0.6 -
3．銅仁市某校為響應國家“雙減”政策（減輕學生作業負擔、減輕校外培訓負擔），落實教育部“五項管理”（作業、睡眠、手機、讀物、體質）工作要求，以便根據學校學生實際情況制定相應措施，隨機抽取50名學生進行問卷調查，并將調查結果制成不完整的統計表（如表）．則m的值是（ ）
作業時間頻數分布組別 作業時間（單位：分鐘） 頻數 A 60＜t≤70 8 B 70＜t≤80 17 C 80＜t≤90 m D t＞90 5 組卷：161引用：2難度：0.5 -
4．估計
的結果應在（ ）（27+6）×13組卷：30引用：2難度：0.7 -
5．已知一次函數y=（m+1）x-2，y的值隨x的增大而減小，則點P（-m,m）所在象限為（ ）
組卷：342引用：3難度：0.5 -
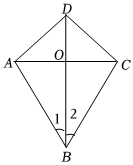6．等腰三角形“三線合一”是應用特別廣泛的一個重要模型，小明對與其相關的習題解題熱情高漲．如圖，四邊形ABCD的對角線AC、BD交于點O，小明根據所給條件依次進行了探究，在其得出的四個命題中，假命題的是（ ）組卷：93引用：3難度：0.5 -
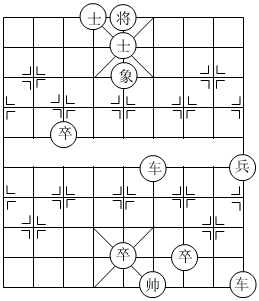7．中國象棋文化歷史久遠，雅俗共賞，具有廣泛的參與度．象棋殘局是象棋的基礎，《七星聚會》素有“殘局之王”的稱謂，深受廣大棋迷喜愛．如圖就是殘局《七星聚會》．如果建立平面直角坐標系，使“帥”位于點（-1，-2），“象”位于點（-2，5），那么“兵”在同一坐標系下的坐標是（ ）組卷：212引用：3難度：0.5 -
8．成書于大約公元前1世紀的《周髀算經》是中國現存最早的一部數學典籍，里面記載的勾股定理的公式與證明相傳是在西周由商高發現，故又稱之為商高定理．觀察下列勾股數：3，4，5；5，12，13；7，24，25；…，這類勾股數的特點是：勾為奇數，弦與股相差為1；古希臘哲學家柏拉圖（公元前427年—公元前347年）研究了勾為2m（m≥3，m為正整數），弦與股相差為2的一類勾股數，如：6，8，10；8，15，17；…，若此類勾股數的勾為12，則其股為（ ）組卷：232引用：6難度：0.5
三、解答題：共9道題，17，18，19，20，21，22每題10分，23，24每題12分，25題14分，共98分.
-
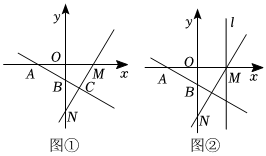24．如圖①，在平面直角坐標系中，直線MN交x軸正半軸于點M，交y軸負半軸于點N（0，-6），∠ONM=30°，作線段MN的垂直平分線交x軸于點A，交y軸于點B，交MN于點C．
（1）求AM的長；
（2）如圖②，過點M作y軸的平行線l,在l上是否存在一點P，使得△PAN的周長最小？若存在，求出點P的坐標；若不存在，說明理由．組卷：116引用：2難度：0.5 -
25．（1）閱讀理解
由兩個頂角相等且有公共頂角頂點的特殊多邊形組成的圖形，如果把它們的底角頂點連接起來，則在相對位置變化的過程中，始終存在一對全等三角形，我們把這種模型稱為“手拉手模型”．在如圖①所示的“手拉手”圖形中，小白發現若∠BAC=∠DAE，AB=AC，AD=AE，則△ABD≌△ACE，請證明他的發現；
（2）問題解決
如圖②，∠BAC=∠DAE=90°，AB=AC，AD=AE，試探索線段CD，BD，DE之間滿足的等量關系，并證明；
（3）拓展探究
如圖③，△ABC和△DEC是擁有公共頂點C的兩個等邊三角形，M點、N點、F點分別是DE、AB、AE的中點．當AD=10時，請直接寫出MN的長．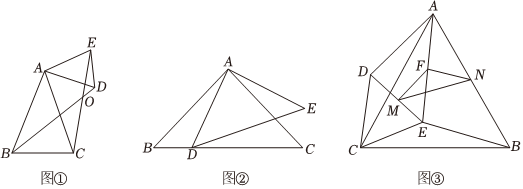
組卷：362引用：2難度：0.5