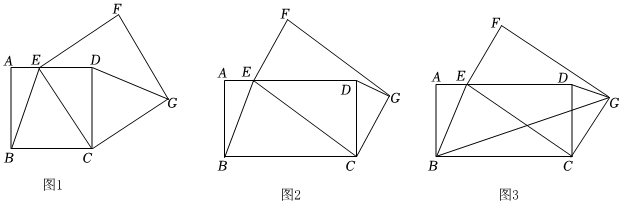
（1）如圖1，四邊形ABCD是正方形，點E是AD邊上的一個動點，以CE為邊在CE的右側作正方形CEFG，連接DG、BE，判斷線段DG與BE的數量關系并說明理由；
（2）如圖2，四邊形ABCD是矩形，AB=3，BC=6，點E是AD邊上的一個動點，以CE為邊在CE的右側作矩形CEFG，且CG：CE=1：2，連接DG、BE．判斷線段DG與BE又有怎樣的數量關系，并說明理由；
（3）如圖3，在（2）的條件下，連接BG，求2BG+BE的最小值．
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/3 19:30:1組卷：520引用：5難度：0.3
相似題
-
1．如圖，在平面直角坐標系中，△BOC是以BO為底邊的等腰三角形，點B在x
軸正半軸上，∠BOC=30°，OB=2，△OCD是△OCB沿OC翻折得到的，點A在y軸正半軸上，連接DA，線段OA的長為x使代數式3-32-x成立．5x-10
（1）求點C的坐標；
（2）求出四邊形OADC是怎樣特殊的四邊形？并且計算四邊形OADC的面積；
（3）平面內是否存在點P，使以點 C、O、B、P為頂點的四邊形是平行四邊形？若存在，請直接寫出點P的坐標；若不存在，請說明理由．發布：2025/6/5 14:30:1組卷：53引用：1難度：0.1 -
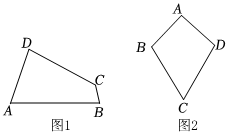2．我們給出定義：有一組對角相等而另一組對角不相等的凸四邊形叫做“等對角四邊形”．
（1）已知：如圖1，四邊形ABCD是“等對角四邊形”，∠A≠∠C，∠A=75°，∠B=80°．求∠C，∠D的度數．
（2）在探究“等對角四邊形”性質時：
①小紅畫了一個“等對角四邊形”ABCD（如圖2），其中∠ABC=∠ADC，AB=AD，此時她發現CB=CD成立．請你證明此結論．
②由此小紅猜想：“對于任意‘等對角四邊形’，當一組鄰邊相等時，另一組鄰邊也相等”．你認為她的猜想正確嗎？若正確，請證明；若不正確，請舉出反例．
（3）已知：在“等對角四邊形”ABCD中，∠DAB=60°，∠ABC=90°，AB=7，AD=5．求對角線AC的長．發布：2025/6/5 13:0:2組卷：109引用：2難度：0.3 -
3．【問題探究】：如圖1，銳角△ABC中，分別以AB、AC為邊向外作正方形ABED和正方形ACFG，連接BG、CD交于點H，試猜想線段BG與線段CD的數量及位置關系，并說明理由；
【拓展應用】：
（1）在【問題探究】的條件下，如圖1，連接DG，若AB=6，AC=4，則BC2+DG2=；
（2）如圖2，在△ABC中，∠ACB=45°，以AB為直角邊，A為直角頂點向外作等腰直角△ABD，連接CD，若AC=，BC=4，則CD長為 ；6
（3）如圖3，已知在平面直角坐標系xOy中，O為坐標原點，、P（2，0），過點P作直線l⊥x軸，點B是直線l上的一個動點，線段AB繞點A按逆時針方向旋轉30°得到線段AC，則AC+PC的最小值為 ．A（0，23）
發布：2025/6/5 13:30:2組卷：158引用：1難度：0.1