（1）如圖1，在三角形ABC中，AC=BC=2，AB=23，求證：∠C=120°；
（2）如圖2，已知菱形ABCD中，∠BAD=60°，AD=8，P、M分別為AC、AD上的兩個動點（均不與A重合），且始終有PA=3AM，點N為菱形內部一點，連接MN交AC于點E，恰好∠PEN=60°，PE=2EN=2x,若用y表示陰影部分的面積之和，即y=S△PDM+S△ABN，回答下列兩個問題：
①直接寫出x的取值范圍；
②求y與x的函數關系式，并求出陰影部分面積的最大值．
AB
=
2
3
PA
=
3
AM
【考點】四邊形綜合題．
【答案】（1）證明見解析過程；
（2）①；
②；陰影部分面積最大值為．
（2）①
0
＜
x
＜
4
3
3
②
y
=
-
3
3
x
2
+
18
x
9
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/11 4:0:9組卷：23引用：2難度：0.5
相似題
-
1．如圖所示，在平行四邊形ABCD中，∠DAC=60°，點E是BC邊上一點，連接AE，AE=AB，點F是對角線AC邊上一動點，連接EF．
（1）如圖1，若點F與對角線交點O重合，已知BE=4，OC：EC=5：3，求AC的長度；
（2）如圖2，若EC=FC，點G是AC邊上一點，連接BG、EG，已知∠AEG=60°，∠AGB+∠BCD=180°，求證：BG+EG=DC．
（3）如圖3，若BE=4，CE=，將EF繞點E逆時針旋轉90°得EF'，請直接寫出當AF'+433BF'取得最小值時△ABF′的面積．12
發布：2025/6/21 23:30:2組卷：402引用：1難度：0.4 -
2．平行四邊形ABCD中，AB⊥AC，點E在邊AD上，連BE．
（1）如圖1，AC交BE于點G，若BE平分∠ABC，且∠DAC=30°，CG=2，請求出四邊形EGCD的面積；
（2）如圖2，點F在對角線AC上，且AF=AB，連BF，過點F作FH⊥BE于H，連AH并延長交CD于點M，點N在邊AD上，連MN．若AN=BF，2∠NMD=∠DAC+∠HBF，求證：HF+AH=AC．2
（3）如圖3，線段PO在線段BE上運動，點R在邊BC上，連接CQ、PR．若BE平分∠ABC，∠DAC=30°，AB=，PQ=3，BC=4BR．請直接寫出線段CQ+PQ+PR的和的最小值以及此時△CQE的面積．32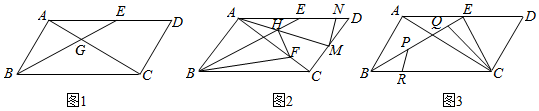
發布：2025/6/22 1:0:1組卷：261引用：3難度：0.5 -
3．如圖，四邊形ABCD是平行四邊形，點E、F在BC上，且CF=BE，連接DE，過點F作FG⊥AB于點G．
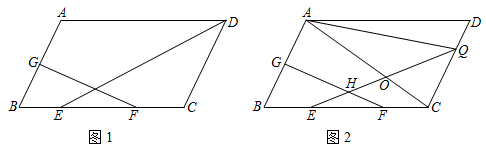
（1）如圖1，若∠B=60°，DE平分∠ADC，且CD=2CF，CD=6，求平行四邊形ABCD的面積．3
（2）點H在GF上，且HE=HF，延長EH交AC，CD于點O，Q，連接AQ，若AC=BC=EQ，∠EQC=45°，求證：CE=BG+DQ．2發布：2025/6/21 23:0:2組卷：155引用：1難度：0.1